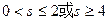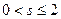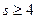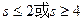题目内容
两种大小不同的钢板可按下表截成A,B,C三种规格成品:
某建筑工地需A,B,C三种规格的成品分别为15,18,27块,问怎样截这两种钢板,可得所需三种规格成品,且所用钢板张数最小.
 | A规格 | B规格 | C规格 |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |
要截得所需三种规格的钢板,且使所截两种钢板的张数最少的方法有两种:
第一种截法是截第一种钢板3张,第二种钢板9张;
第二种截法是截第一种钢板4张,第二种钢板8张;
两种方法都最少要截两种钢板共12张.
第一种截法是截第一种钢板3张,第二种钢板9张;
第二种截法是截第一种钢板4张,第二种钢板8张;
两种方法都最少要截两种钢板共12张.
设需要第一种钢板x张,第二种钢板y张,钢板总数为z张,z=x+y,
 约束条件为:
约束条件为: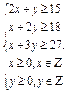
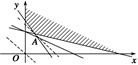
作出可行域如图所示:
令z=0,作出基准直线l:y=-x,平行移动直线l发现在可行域内,经过直线x+3y=27和直线2x+y=15的交点A 可使z取最小,由于
可使z取最小,由于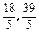 都不是整数,而最优解(x,y)中,x,y必须都是整数,可行域内点A
都不是整数,而最优解(x,y)中,x,y必须都是整数,可行域内点A 不是最优解;
不是最优解;
通过在可行域内画网格发现,经过可行域内的整点且与A 点距离最近的直线是x+y=12,经过的整点是B(3,9)和C(4,8),它们都是最优解.
点距离最近的直线是x+y=12,经过的整点是B(3,9)和C(4,8),它们都是最优解.
答 要截得所需三种规格的钢板,且使所截两种钢板的张数最少的方法有两种:
第一种截法是截第一种钢板3张,第二种钢板9张;
第二种截法是截第一种钢板4张,第二种钢板8张;
两种方法都最少要截两种钢板共12张.
 约束条件为:
约束条件为: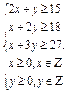
作出可行域如图所示:
令z=0,作出基准直线l:y=-x,平行移动直线l发现在可行域内,经过直线x+3y=27和直线2x+y=15的交点A
 可使z取最小,由于
可使z取最小,由于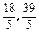 都不是整数,而最优解(x,y)中,x,y必须都是整数,可行域内点A
都不是整数,而最优解(x,y)中,x,y必须都是整数,可行域内点A 不是最优解;
不是最优解;通过在可行域内画网格发现,经过可行域内的整点且与A
 点距离最近的直线是x+y=12,经过的整点是B(3,9)和C(4,8),它们都是最优解.
点距离最近的直线是x+y=12,经过的整点是B(3,9)和C(4,8),它们都是最优解.答 要截得所需三种规格的钢板,且使所截两种钢板的张数最少的方法有两种:
第一种截法是截第一种钢板3张,第二种钢板9张;
第二种截法是截第一种钢板4张,第二种钢板8张;
两种方法都最少要截两种钢板共12张.

练习册系列答案
相关题目
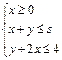 下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是( )
下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是( )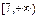
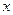 的实系数方程
的实系数方程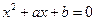 有两个根,一个根在区间
有两个根,一个根在区间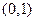 内,另一根在区间
内,另一根在区间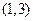 内,记点
内,记点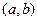 对应的区域为
对应的区域为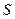 .
.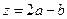 ,求
,求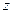 的取值范围;
的取值范围;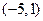 的一束光线,射到
的一束光线,射到 经过区域
经过区域 在平面直角坐标系中,有两个区域M、N,M是由三个不等式y≥0、y≤x和y≤2-x确定的;N是随t变化的区域,它由不等式t≤x≤t+1(0≤t≤1)所确定.设M、N的公共部分的面积为f(t),则f(t)等于
在平面直角坐标系中,有两个区域M、N,M是由三个不等式y≥0、y≤x和y≤2-x确定的;N是随t变化的区域,它由不等式t≤x≤t+1(0≤t≤1)所确定.设M、N的公共部分的面积为f(t),则f(t)等于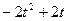
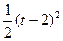
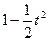
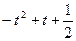
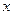 、
、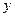 满足条件
满足条件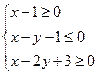 ,则
,则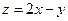 的最小值为 .
的最小值为 .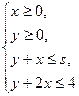 表示的平面区域是一个三角形,则实数s的取值范围是( )
表示的平面区域是一个三角形,则实数s的取值范围是( )