题目内容
(2009•潍坊二模)某工厂生产一种精密仪器,产品是否合格需先后经两道相互独立的工序检查,且当第一道工序检查合格后才能进人第二道工序经长期监测发现,该仪器第一道工序检查合格的概率为号,第二道工序检查合格的概率为云已知该厂每月生产3台这种仪器.
(I)求每生产一台合格仪器的概率;
(II)用f表示每月生产合格仪器的台数,求f的分布列和数学期望;
(Ⅲ)若生产一台仪器合格可盈利l0万元,不合格要亏损3万元,求该厂每月的期望盈利额.
(I)求每生产一台合格仪器的概率;
(II)用f表示每月生产合格仪器的台数,求f的分布列和数学期望;
(Ⅲ)若生产一台仪器合格可盈利l0万元,不合格要亏损3万元,求该厂每月的期望盈利额.
分析:(I)设“生产一台仪器合格”为事件A,独立重复试验的概率公式得到每生产一台合格仪器的概率;
(II)根据题意得到变量的可能的取值,根据变量对应的事件,利用独立重复试验的概率公式得到概率,写出分布列,根据做出的变量的分布列,代入求期望值的公式做出期望值;
(III)该厂生产一件仪器合格率为
,不合格率为
,从而得出每台期望盈利,最后即可得到该厂每月的期望盈利额.
(II)根据题意得到变量的可能的取值,根据变量对应的事件,利用独立重复试验的概率公式得到概率,写出分布列,根据做出的变量的分布列,代入求期望值的公式做出期望值;
(III)该厂生产一件仪器合格率为
| 4 |
| 5 |
| 1 |
| 5 |
解答:解:(I)设“生产一台仪器合格”为事件A,则P(A)=
×
=
;
(II)每月生产合格仪器的数量ξ可为:3,2,1,0.则
P(ξ=3)=
(
)3=
,
P(ξ=2)=
(
)2(
)=
,
P(ξ=3)=
(
) (
)2=
,
P(ξ=3)=
(
)3=
.
∴ξ的分布列为:
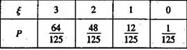
Eξ=3×
+2×
+1×
+0×
=
.
(III)该厂生产一件仪器合格率为
,不合格率为
,∴每台期望盈利为10×
-3×
=7.4(万元),
∴该厂每月的期望盈利额7.4×3=22.2万元.
| 8 |
| 9 |
| 9 |
| 10 |
| 4 |
| 5 |
(II)每月生产合格仪器的数量ξ可为:3,2,1,0.则
P(ξ=3)=
| C | 3 3 |
| 4 |
| 5 |
| 64 |
| 125 |
P(ξ=2)=
| C | 2 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 48 |
| 125 |
P(ξ=3)=
| C | 1 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 12 |
| 125 |
P(ξ=3)=
| C | 0 3 |
| 1 |
| 5 |
| 1 |
| 125 |
∴ξ的分布列为:

Eξ=3×
| 64 |
| 125 |
| 48 |
| 125 |
| 12 |
| 125 |
| 1 |
| 125 |
| 12 |
| 5 |
(III)该厂生产一件仪器合格率为
| 4 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
∴该厂每月的期望盈利额7.4×3=22.2万元.
点评:本题考查离散型随机变量的分布列和期望,独立重复试验的概率公式,本题解题的关键是看出所给的变量符合什么规律,利用概率的公式来解题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目