题目内容
(2009•潍坊二模)给出下列结论:
①函数y=tan
在区间(-π,π)上是增函数;
②不等式|2x-1|>3的解集是{x|x>2};
③m=
是两直线2x+my+1=0与mx+y-1=0平行的充分不必要条件;
④函数y=x|x-2|的图象与直线y=
有三个交点.
其中正确结论的序号是
①函数y=tan
| x |
| 2 |
②不等式|2x-1|>3的解集是{x|x>2};
③m=
| 2 |
④函数y=x|x-2|的图象与直线y=
| 1 |
| 2 |
其中正确结论的序号是
①③④
①③④
(把所有正确结论的序号都填上)分析:①利用正切函数的性质判断①的正误;②不等式|2x-1|>3的解集是{x|x>2,或x<-1};③利用两条直线平行的性质判断③的正误;④作出函数的图象,数形结合能够判断④的正误.
解答: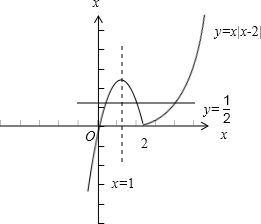 解:①∵x∈(-π,π),∴
解:①∵x∈(-π,π),∴
∈(-
,
),
∴函数y=tan
在区间(-π,π)上是增函数,故①正确;
②不等式|2x-1|>3的解集是{x|x>2,或x<-1},故②不正确;
③∵m=
⇒两直线2x+my+1=0与mx+y-1=0平行,
两直线2x+my+1=0与mx+y-1=0平行⇒m=±
,
∴m=
是两直线2x+my+1=0与mx+y-1=0平行的充分不必要条件,故③正确;
④作出函数y=x|x-2|=
和y=
的图象:
由图象知函数y=x|x-2|的图象与直线y=
有三个交点,
故④正确.
故答案为:①③④.
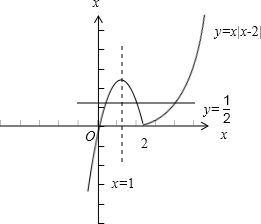 解:①∵x∈(-π,π),∴
解:①∵x∈(-π,π),∴| x |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴函数y=tan
| x |
| 2 |
②不等式|2x-1|>3的解集是{x|x>2,或x<-1},故②不正确;
③∵m=
| 2 |
两直线2x+my+1=0与mx+y-1=0平行⇒m=±
| 2 |
∴m=
| 2 |
④作出函数y=x|x-2|=
|
| 1 |
| 2 |
由图象知函数y=x|x-2|的图象与直线y=
| 1 |
| 2 |
故④正确.
故答案为:①③④.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,注意三角函数、直线的位置关系、含绝对值的不等式、分段函数等知识点的合理运用.

练习册系列答案
相关题目