题目内容
5.已知α,β为锐角,cosα=$\frac{4}{5}$,tan(α-β)=-$\frac{1}{3}$,则cosβ=$\frac{9\sqrt{10}}{50}$;已知α,β为锐角,cosα=$\frac{1}{7}$,cos(β+α)=-$\frac{11}{14}$,则cosβ=$\frac{1}{2}$.
分析 (1)利用同角三角函数的基本关系求出sinα 的值,可得tanα 的值,根据 tan(α-β)=-$\frac{1}{3}$,利用两角差的正切公式解方程求得tanβ 的值,由同角三角函数关系式即可求cosβ的值;
(2)先利用同角三角函数的基本关系求得sinα和sin(α+β)的值,然后利用cosβ=cos[(α+β)-α],根据两角和公式求得答案.
解答 解:(1)已知α,β为锐角,cosα=$\frac{4}{5}$,∴sinα=$\frac{3}{5}$,tanα=$\frac{3}{4}$.
∵tan(α-β)=-$\frac{1}{3}$,
∴$\frac{\frac{3}{4}-tanβ}{1+\frac{3}{4}×tanβ}$=-$\frac{1}{3}$,解得 tanβ=$\frac{13}{9}$,
∴cosβ=$\sqrt{\frac{1}{1+ta{n}^{2}β}}$=$\sqrt{\frac{1}{1+\frac{169}{81}}}$=$\frac{9\sqrt{10}}{50}$.
(2)∵α,β均为锐角,
∴sinα=$\sqrt{1-\frac{1}{49}}$=$\frac{4\sqrt{3}}{7}$,sin(α+β)=$\sqrt{1-(\frac{11}{14})^{2}}$=$\frac{5\sqrt{3}}{14}$,
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=$\frac{1}{2}$.
故答案为:$\frac{9\sqrt{10}}{50}$,$\frac{1}{2}$.
点评 本题主要考查了两角和公式的化简求值和同角三角函数的基本关系的应用.熟练记忆三角函数的基本公式是解题的基础.属于基本知识的考查.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案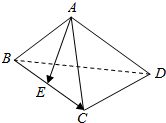
| A. | $\overrightarrow{AE}•\overrightarrow{BC}$<$\overrightarrow{AE}•\overrightarrow{CD}$ | B. | $\overrightarrow{AE}•\overrightarrow{BC}$=$\overrightarrow{AE}•\overrightarrow{CD}$ | ||
| C. | $\overrightarrow{AE}•\overrightarrow{BC}$>$\overrightarrow{AE}•\overrightarrow{CD}$ | D. | $\overrightarrow{AE}•\overrightarrow{BC}$与$\overrightarrow{AE}•\overrightarrow{CD}$大小不确定 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |