题目内容
对于任意两个正整数m,n,定义某种运算“※”,法则如下:当m,n都是正奇数时,m※n=m+n;当m,n不全为正奇数时,m※n=mn.则在此定义下,集合M={(a,b)|a※b=16,a∈N*,b∈N*}中的元素个数是( )
| A、7 | B、11 | C、13 | D、14 |
考点:元素与集合关系的判断
专题:集合
分析:由所给的定义,对a※b=16,a∈N*,b∈N*进行分类讨论,分两个数都是正奇数,与两个数不全为正奇数,两类进行讨论,即可确定出元素的个数
解答:解:由题意,当m,n都是正奇数时,m※n=m+n;当m,n不全为正奇数时,m※n=mn;
若a,b都是正奇数,则由a※b=16,可得a+b=16,此时符合条件的数对为(1,15),(3,13),…(15,1)满足条件的共8个;
若m,n不全为正奇数时,m※n=mn,由a※b=16,可得ab=16,则符合条件的数对分别为(1,16),(2,8),(4,4),(8,2),(16,1)共5个;
故集合M={(a,b)|a※b=16,a∈N*,b∈N*}中的元素个数是13.
故选:C.
若a,b都是正奇数,则由a※b=16,可得a+b=16,此时符合条件的数对为(1,15),(3,13),…(15,1)满足条件的共8个;
若m,n不全为正奇数时,m※n=mn,由a※b=16,可得ab=16,则符合条件的数对分别为(1,16),(2,8),(4,4),(8,2),(16,1)共5个;
故集合M={(a,b)|a※b=16,a∈N*,b∈N*}中的元素个数是13.
故选:C.
点评:本题考查元素与集合关系的判断,正确解答本量题的关键是正确理解所给的定义及熟练运用分类讨论的思想进行列举,本题属于基本题,

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
已知集合A={x|x2-3x+a>0,x∈R},且1∉A,则实数a的取值范围是( )
| A、(-∞,2] | B、[2,+∞) | C、(-∞,-2] | D、[-2,+∞) |
已知集合A={0,1,2,3},B={(x,y)|x∈A,y∈A,|x-y|∈A},则B中所含元素的个数为( )
| A、14 | B、16 | C、28 | D、32 |
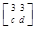 ,若矩阵A属于特征值6的一个特征向量为α1=
,若矩阵A属于特征值6的一个特征向量为α1=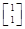 ,属于特征值1的一个特征向量为α2=
,属于特征值1的一个特征向量为α2= .求矩阵A,并写出A的逆矩阵.
.求矩阵A,并写出A的逆矩阵. (
( )任意排成
)任意排成 行
行 (
( )的比值
)的比值 ,称这些比值中的最小值为这个数表的“特征值”.若
,称这些比值中的最小值为这个数表的“特征值”.若 表示某个
表示某个 行第
行第 列的数(
列的数( ,
,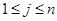 ),且满足
),且满足 ,当
,当 时数表的“特征值”为_________
时数表的“特征值”为_________ 中,元素
中,元素 的代数余子式的值是 .
的代数余子式的值是 . 对应变换的作用下得到的点为B(-1,1),求矩阵M的逆矩阵.
对应变换的作用下得到的点为B(-1,1),求矩阵M的逆矩阵.