题目内容
18.若4x-5×2x+4≤0,求y=($\frac{1}{9}$)x-4×($\frac{1}{3}$)x+2的最大值与最小值.分析 根据指数不等式的解法先求出x的取值范围,利用换元法转化为一元二次函数进行求解即可.
解答 解:若4x-5×2x+4≤0,
则若(2x)2-5×2x+4≤0,
即(2x-1)(2x-4)≤0,
即1≤2x≤4,即0≤x≤2,
则y=($\frac{1}{9}$)x-4×($\frac{1}{3}$)x+2=y=[($\frac{1}{3}$)x]2-4×($\frac{1}{3}$)x+2,
设t=($\frac{1}{3}$)x,则$\frac{1}{9}$≤t≤1,
则函数等价为y=t2-4t+2=(t-2)2-2,
则函在$\frac{1}{9}$≤t≤1,上为减函数,
则当t=1时,函数取得最小值为y=1-4+2=-1,
当t=$\frac{1}{9}$时,函数取得最大值为y=($\frac{1}{9}$)2-4×$\frac{1}{9}$+2=$\frac{127}{81}$.
点评 本题主要考查复合函数单调性和最值的求解,利用换元法转化为一元二次函数是解决本题的关键.

练习册系列答案
相关题目
6.函数y=3x(x∈N,1≤x≤5)的图象是( )
| A. | 直线 | B. | 射线 | C. | 线段 | D. | 离散的点 |
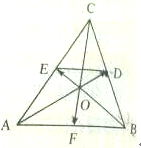 如图所示,已知△ABC中,D,E,F分别是BC,CA,AB的中点.且AD与BE交于O点.求证:$\overrightarrow{AD}$+$\overrightarrow{BE}$+$\overrightarrow{CF}$=$\overrightarrow{0}$.
如图所示,已知△ABC中,D,E,F分别是BC,CA,AB的中点.且AD与BE交于O点.求证:$\overrightarrow{AD}$+$\overrightarrow{BE}$+$\overrightarrow{CF}$=$\overrightarrow{0}$.