Question

【题目】如图，是边长为2的正方形，平面平面，且，是线段的中点，过作直线，是直线上一动点.

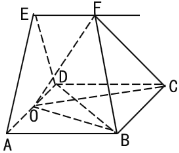
（1）求证：；

（2）若直线上存在唯一一点使得直线与平面垂直，求此时二面角的余弦值.

Answer 1

【答案】(1)见解析;(2)

【解析】

（1）先证EO⊥面ABCD，进而可得BC⊥面EOF，从而可证OF⊥BC；

（2）由（1）可得平面，得到、、两两垂直，可建立空间直角坐标系，由条件得到，转化为向量，从而，转化为关于的方程有唯一实数解，得到，，又判断∠BFC为二面角B﹣OF﹣C的平面角，利用向量夹角公式可求二面角B﹣OF﹣C的余弦值．

（1）因为，是中点，故，

又因为平面平面，平面平面，

故平面，所以；

因为，，所以，

故平面，

所以.

（2）设的中点为，则有，由（1），平面，

所以、、两两垂直.可如图建立空间直角坐标系.

依题意设点的坐标为，点的坐标为，又，，

所以，，

由（1）知，故与平面垂直，等价于，

故，从而，即，

直线上存在唯一一点使得直线与平面垂直，即关于的方程有唯一实数解.

所以，解得，此时.

故点的坐标为，点的坐标为.

因为平面，所以且，

所以即二面角的平面角.

因为，，

所以，

即若直线上存在唯一一点使得直线与平面垂直时，

所以二面角的余弦值为.