题目内容
(本小题满分12分)
已知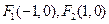 ,点
,点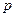 满足
满足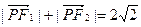 ,记点
,记点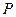 的轨迹
的轨迹 为
为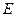 .
.
(Ⅰ)求轨迹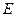 的方程;
的方程;
(Ⅱ)过点F2(1 ,0)作直线l与轨迹
,0)作直线l与轨迹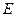 交于不同的两点A、B,设
交于不同的两点A、B,设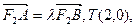
 ,若
,若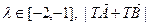 的取值范围
的取值范围
已知
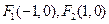 ,点
,点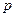 满足
满足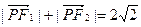 ,记点
,记点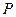 的轨迹
的轨迹 为
为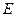 .
.(Ⅰ)求轨迹
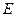 的方程;
的方程;(Ⅱ)过点F2(1
 ,0)作直线l与轨迹
,0)作直线l与轨迹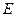 交于不同的两点A、B,设
交于不同的两点A、B,设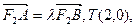
 ,若
,若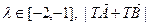 的取值范围
的取值范围(Ⅰ)
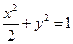
(Ⅱ)
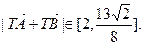
解:(Ⅰ)由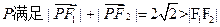 知,点P的轨迹为以
知,点P的轨迹为以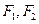 为焦点,长轴长为
为焦点,长轴长为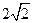 的椭圆
的椭圆
所以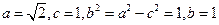
轨迹方程为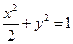 . ------------------------(6分)
. ------------------------(6分)
(Ⅱ)根据题设条件可设直线l的方程为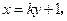
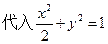 中,得
中,得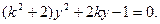
设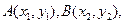
则由根与系数的关系,得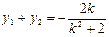 ①
①
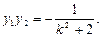 ②
②
 ∵
∵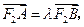 ∴有
∴有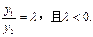
将①式平方除以②式,得
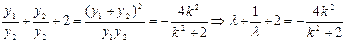
由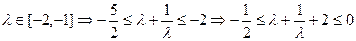
 ------------------(9分)
------------------(9分)
 ∵
∵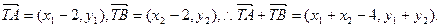
又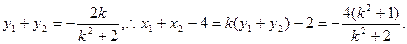
故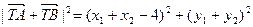
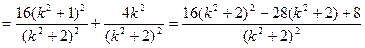
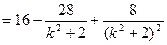
令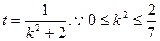 ∴
∴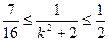 ,即
,即 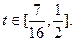
∴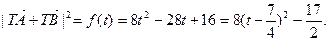
而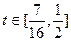 , ∴
, ∴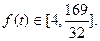
∴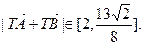 ----------
---------- ----------(12分)
----------(12分)
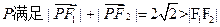 知,点P的轨迹为以
知,点P的轨迹为以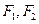 为焦点,长轴长为
为焦点,长轴长为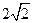 的椭圆
的椭圆所以
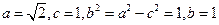
轨迹方程为
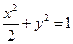 . ------------------------(6分)
. ------------------------(6分)(Ⅱ)根据题设条件可设直线l的方程为
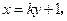
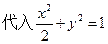 中,得
中,得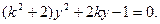
设
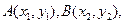
则由根与系数的关系,得
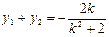 ①
① 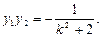 ②
②  ∵
∵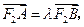 ∴有
∴有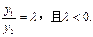
将①式平方除以②式,得
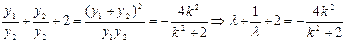
由
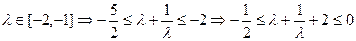
 ------------------(9分)
------------------(9分) ∵
∵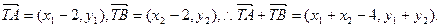
又
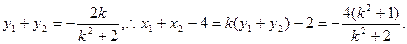
故
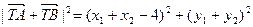
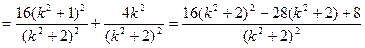
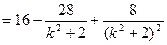
令
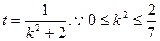 ∴
∴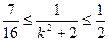 ,即
,即 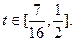
∴
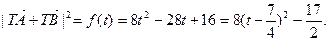
而
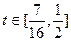 , ∴
, ∴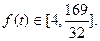
∴
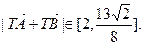 ----------
---------- ----------(12分)
----------(12分)
练习册系列答案
相关题目
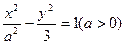 的两个焦点分别为
的两个焦点分别为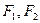 ,离心率为
,离心率为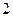 .
.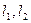 的方程;
的方程;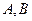 分别为
分别为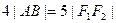 ,求线段
,求线段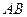 的中点
的中点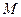 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线. 足条件
足条件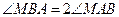 ,求动
,求动 点M的轨迹方程并指出轨迹是什么图形
点M的轨迹方程并指出轨迹是什么图形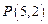 、
、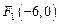 、
、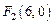 .
.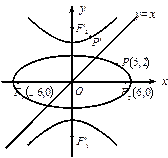
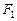 、
、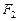 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;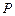 、
、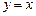 的对称点分别为
的对称点分别为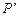 、
、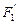 、
、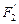 ,求以
,求以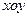 中,设点
中,设点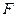 (1,0),直线
(1,0),直线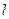 :
: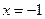 ,点
,点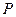 在直线
在直线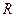 是线段
是线段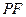 与
与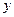 轴的交点,
轴的交点, 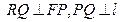 .
.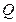 的轨迹的方程;
的轨迹的方程;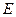 ,过点
,过点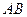 、
、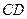 ,设
,设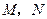 .求证:直线
.求证:直线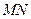 必过定点
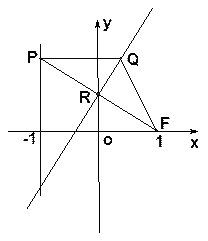
必过定点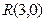 .
.
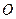 为坐标原点,点F、T、M、P分别满足
为坐标原点,点F、T、M、P分别满足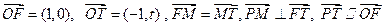 .
. 的顶点在点P的轨迹上,且点A的纵坐标
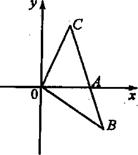
的顶点在点P的轨迹上,且点A的纵坐标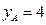 ,
,
 分10分)
分10分)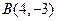 ,点
,点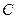 在第一象限内,
在第一象限内,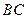 交
交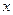 轴于点
轴于点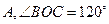 ,
,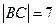 .
.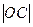 的长;
的长;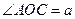 ,
,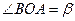 .(
.(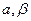 为锐角),求sina,sin
为锐角),求sina,sin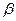 的值
的值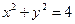 ,直线
,直线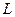 交⊙O于A、B两点,分别过A、B作⊙O的切线,交于M点。
交⊙O于A、B两点,分别过A、B作⊙O的切线,交于M点。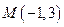 时,求弦长AB;
时,求弦长AB;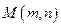 的轨迹
的轨迹 方程。
方程。