��Ŀ����
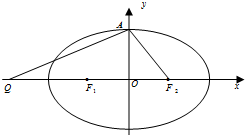 ����ԲC��
����ԲC��| x2 |
| a2 |
| y2 |
| b2 |
| F1F2 |
| F2Q |
| 0 |
��1������ԲC�������ʣ�
��2������A��Q��F2�����Բǡ����ֱ��l��x-
| 3 |
��3���ڣ�2���������£����ҽ���F2��б��Ϊk��ֱ��l����ԲC����M��N���㣬��x�����Ƿ���ڵ�P��m��0��ʹ����PM��PNΪ�ڱߵ�ƽ���ı��������Σ�������ڣ����m��ȡֵ��Χ����������ڣ�˵�����ɣ�
��
��������1����Q��x0��0������F2��c��0����A��0��b�����������������������ó�����a��c�ĵ�ʽ���Ӷ������Բ�������ʼ��ɣ�
��2���ɣ�1��֪a��c��һ�����̣������á�AQF�����Բ�ó���һ�����̣���������������ɵķ����鼴�����������Բ���̣�
��3���ɣ���ֱ֪��l��y=k��x-1������ֱ�ߵķ��̴�����Բ�ķ��̣���ȥy�õ�����x��һԪ���η��̣��ٽ�ϸ�ϵ���Ĺ�ϵ�����ҳ���ʽ���������������ĵ�P��m��ȡֵ��Χ��
��2���ɣ�1��֪a��c��һ�����̣������á�AQF�����Բ�ó���һ�����̣���������������ɵķ����鼴�����������Բ���̣�
��3���ɣ���ֱ֪��l��y=k��x-1������ֱ�ߵķ��̴�����Բ�ķ��̣���ȥy�õ�����x��һԪ���η��̣��ٽ�ϸ�ϵ���Ĺ�ϵ�����ҳ���ʽ���������������ĵ�P��m��ȡֵ��Χ��
����⣺��1����Q��x0��0������F2��c��0����A��0��b��
֪
=(-c��b)��
=(x0��-b)
��
��
����-cx0-b2=0��x0=-
��
����2
+
=
��F1ΪF2Q�е㣮
��-
+c=-2c��b2=3c2=a2-c2��
����Բ��������e=
����3�֣�
��2���ɣ�1��֪
=
����c=
a����F2��
a��0��Q(-
a��0)��
��AQF�����ԲԲ��Ϊ��-
a��0�����뾶r=
|FQ|=a
����
=a�����a=2����c=1��b=
��
������Բ����Ϊ
+
=1����6�֣�
��3���ɣ���֪F2��1��0��l��y=k��x-1��
����ã�3+4k2��x2-8k2x+4k2-12=0
��M��x1��y1����N��x2��y2��
��x1+x2=
��y1+y2=k��x1+x2-2������8�֣�
+
=(x1-m��y1)+(x2-m��y2)=��x1+x2-2m��y1+y2��
�������ζԽ��ߴ�ֱ����(
+
)•
=0
��k��y1+y2��+x1+x2-2m=0
��k2��x1+x2-2��+x1+x2-2m=0k2(
-2)+
-2m=0��10�֣�
����֪����֪k��0��k��R��m=
=
��0��m��
�ʴ�����������ĵ�P��m��ȡֵ��Χ��0��m��
����12�֣�
֪
| F2A |
| AQ |
��
| F2A |
| AQ |
| b2 |
| c |
����2
| F1F2 |
| F2Q |
| 0 |
��-
| b2 |
| c |
����Բ��������e=
| 1 |
| 2 |
��2���ɣ�1��֪
| c |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
��AQF�����ԲԲ��Ϊ��-
| 1 |
| 2 |
| 1 |
| 2 |
����
|-
| ||
| 2 |
| 3 |
������Բ����Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
��3���ɣ���֪F2��1��0��l��y=k��x-1��
|
����ã�3+4k2��x2-8k2x+4k2-12=0
��M��x1��y1����N��x2��y2��
��x1+x2=
| 8k2 |
| 3+4k2 |
| PM |
| PN |
�������ζԽ��ߴ�ֱ����(
| PM |
| PN |
| MN |
��k��y1+y2��+x1+x2-2m=0
��k2��x1+x2-2��+x1+x2-2m=0k2(
| 8k2 |
| 3+4k2 |
| 8k2 |
| 3+4k2 |
����֪����֪k��0��k��R��m=
| k2 |
| 3+4k2 |
| 1 | ||
|
| 1 |
| 4 |
�ʴ�����������ĵ�P��m��ȡֵ��Χ��0��m��
| 1 |
| 4 |
��������ֱ����Բ�����ཻʱ �漰�ҳ����⣬���á�Τ�ﶨ�����������������ҳ�����Ӧ���ҳ���ʽ�����漰�ҳ����е����⣬���á������������������ֱ�ߵ�б�ʡ��ҵ��е�������ϵ�������ת�� ͬʱ��Ӧ����ھ���Ŀ������������Ѱ����������Ĺ�ϵ���ת�������������°빦����

��ϰ��ϵ�д�
�����Ŀ
 ����ԲC��
����ԲC��