题目内容
3.已知函数f(x)=cosx,若f(x)=m在区间(0,3π)上恰有三个不同的实根,且三个实根从小到大依次成等比数列,则这三个实根之和为( )| A. | $\frac{9π}{2}$ | B. | $\frac{13π}{4}$ | C. | $\frac{7π}{3}$ | D. | $\frac{14π}{3}$ |
分析 由方程可化为函数f(x)=cosx与函数y=m的图象在区间(0,3π)上有三个不同的交点,作函数图象可得x1+x2=2π,x3=2π+x1;从而解得.
解答 解:∵f(x)=m在区间(0,3π)上恰有三个不同的实根,
∴函数f(x)=cosx与函数y=m的图象在区间(0,3π)上有三个不同的交点,
作函数f(x)=cosx与函数y=m在(0,3π)上的图象如下,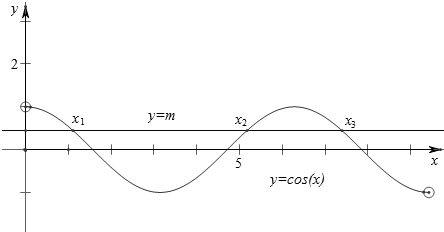
结合图象可得,x1+x2=2π,x3=2π+x1;
又由x1,x2,x3成等比数列知,x22=x1x3,
即(2π-x1)2=x1(2π+x1),
故x1=$\frac{2π}{3}$,
x1+x2+x3=4π+x1=4π+$\frac{2π}{3}$=$\frac{14π}{3}$;
故选D.
点评 本题考查了方程的根与函数的图象的交点的关系应用及等比数列的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,直线x=$\frac{{a}^{2}}{c}$与一条渐近线交于点A,△OAF的面积为$\frac{{a}^{2}}{2}$(O为原点),则两条渐近线的夹角为( )
| A. | 30° | B. | 45° | C. | 90° | D. | 60° |
11.下列说法正确的是( )
(1)残差平方和越小,相关指数R2越小,模型的拟合效果越差
(2)残差平方和越大,相关指数R2越大,模型的拟合效果越好
(3)残差平方和越小,相关指数R2越大,模型的拟合效果越好
(4)残差平方和越大,相关指数R2越小,模型的拟合效果越差.
(1)残差平方和越小,相关指数R2越小,模型的拟合效果越差
(2)残差平方和越大,相关指数R2越大,模型的拟合效果越好
(3)残差平方和越小,相关指数R2越大,模型的拟合效果越好
(4)残差平方和越大,相关指数R2越小,模型的拟合效果越差.
| A. | (1)(2) | B. | (3)(4) | C. | (1)(4) | D. | (2)(3) |
8.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x}(x≤0)}\\{lo{g}_{2}x(x>0)}\end{array}\right.$,则f(f($\frac{1}{2}$))的值是( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
15.用秦九韶算法计算多项式f(x)=x6-12x5+60x4-160x3+240x2-192x+64当x=2时的值 时,v3的值( )
| A. | -10 | B. | -80 | C. | 40 | D. | 80 |
12.设函数f(x)=ax2+c(a≠0),若${∫}_{0}^{1}$f(x)dx=f(x0),0≤x0≤1,则x0的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |