Question

设函数f(x)＝lnx－ax，g(x)＝ex－ax，其中a为实数．

(1)若f(x)在(1，＋∞)上是单调减函数，且g(x)在(1，＋∞)上有最小值，求a的取值范围；

(2)若g(x)在(－1，＋∞)上是单调增函数，试求f(x)的零点个数，并证明你的结论．

 

Answer 1

(1) a∈(e，＋∞)．

(2) 当a≤0或a＝e－1时，f(x)的零点个数为1，当0<a<e－1时，f(x)的零点个数为2. 证明见解析

【解析】【解析】
(1)令f′(x)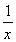＝－a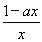＝<0，考虑到f(x)的定义域为(0，＋∞)，故a>0，进而解得x>a－1，即f(x)在(a－1，＋∞)上是单调减函数．同理，f(x)在(0，a－1)上是单调增函数．由于f(x)在(1，＋∞)上是单调减函数，故(1，＋∞)⊆(a－1，＋∞)，从而a－1≤1，即a≥1.令g′(x)＝ex－a＝0，得x＝ln a．当x<ln a时，g′(x)<0；当x>ln a时，g′(x)>0.又g(x)在(1，＋∞)上有最小值，所以ln a>1，即a>e.

综上，有a∈(e，＋∞)．

(2)当a≤0时，g(x)必为单调增函数；当a>0时，令g′(x)＝ex－a>0，

解得a<ex，即x>ln a，因为g(x)在(－1，＋∞)上是单调增函数，类似(1)有ln a≤－1，即0<a≤e－1.结合上述两种情况，有a≤e－1.

(ⅰ)当a＝0时，由f(1)＝0以及f′(x)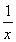＝>0，得f(x)存在唯一的零点；

(ⅱ)当a<0时，由于f(ea)＝a－aea＝a(1－ea)<0，f(1)＝－a>0，且函数f(x)在[ea,1]上的图象不间断，所以f(x)在(ea,1)上存在零点．另外，当x>0时，f′(x)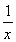＝－a>0，故f(x)在(0，＋∞)上是单调增函数，所以f(x)只有一个零点．

(ⅲ)当0<a≤e－1时，令f′(x)＝－a＝0，解得x＝a－1.当0<x<a－1时，f′(x)>0，当x>a－1时，f′(x)<0，所以，x＝a－1是f(x)的最大值点，且最大值为f(a－1)＝－ln a－1.

①当－ln a－1＝0，即a＝e－1时，f(x)有一个零点x＝e.

②当－ln a－1>0，即0<a<e－1时，f(x)有两个零点．

实际上，对于0<a<e－1，由于f(e－1)＝－1－ae－1<0，f(a－1)>0，且函数f(x)在[e－1，a－1]上的图象不间断，所以f(x)在(e－1，a－1)上存在零点．

另外，当x∈(0，a－1)时，f′(x)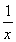＝－a>0，故f(x)在(0，a－1)上是单调增函数，所以f(x)在(0，a－1)上只有一个零点．

下面考虑f(x)在(a－1，＋∞)上的情况．先证f(ea－1)＝a(a－2－ea－1)<0.

为此，我们要证明：当x>e时，ex>x2.设h(x)＝ex－x2，则h′(x)＝ex－2x，再设l(x)＝h′(x)＝ex－2x，则l′(x)＝ex－2.

当x>1时，l′(x)＝ex－2>e－2>0，所以l(x)＝h′(x)在(1，＋∞)上是单调增函数．故当x>2时，h′(x)＝ex－2x>h′(2)＝e2－4>0，从而h(x)在(2，＋∞)上是单调增函数．进而当x>e时，

h(x)＝ex－x2>h(e)＝ee－e2>0.即当x>e时，ex>x2.

当0<a<e－1，即a－1>e时，f(ea－1)＝a－1－aea－1＝a(a－2－ea－1)<0，又f(a－1)>0，且函数f(x)在[a－1，ea－1]上的图象不间断，所以f(x)在(a－1，ea－1)上存在零点．又当x>a－1时，f′(x)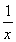＝－a<0，故f(x)在(a－1，＋∞)上是单调减函数，所以f(x)在(a－1，＋∞)上只有一个零点．

综合(ⅰ)，(ⅱ)，(ⅲ)，当a≤0或a＝e－1时，f(x)的零点个数为1，当0<a<e－1时，f(x)的零点个数为2.