题目内容
在各项均为负数的数列{an}中,已知点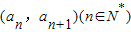 在函数
在函数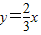 的图象上,且
的图象上,且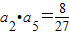 .则数列{an}的通项公式为an= .
.则数列{an}的通项公式为an= .
【答案】分析:根据点(an,an+1)(n∈N*)在函数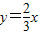 的图象上,可得an+1=
的图象上,可得an+1= an,从而数列{an}是公比为
an,从而数列{an}是公比为 的等比数列,根据a2•a5=
的等比数列,根据a2•a5=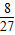 可得数列的首项,从而求出通项公式;
可得数列的首项,从而求出通项公式;
解答:解:∵点(an,an+1)(n∈N*)在函数y=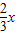 ,可得an+1=
,可得an+1= an,
an,
∴数列{an}是公比为 的等比数列,
的等比数列,
∵a2•a5=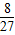 ,
,
∴a1q•a1q4=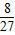 ,
,
∴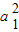 q5=
q5=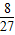 ,可得
,可得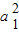 (
( )5=
)5=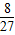 ,a1<0
,a1<0
解得a1=- ,
,
所以an=-( )n-2,
)n-2,
故答案为:以an=-( )n-2
)n-2
点评:本题考查数列与函数的关系,考查数列的通项与求和,确定数列是等比数列是关键,此题是一道基础题;
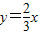 的图象上,可得an+1=
的图象上,可得an+1= an,从而数列{an}是公比为
an,从而数列{an}是公比为 的等比数列,根据a2•a5=
的等比数列,根据a2•a5=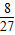 可得数列的首项,从而求出通项公式;
可得数列的首项,从而求出通项公式;解答:解:∵点(an,an+1)(n∈N*)在函数y=
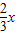 ,可得an+1=
,可得an+1= an,
an,∴数列{an}是公比为
 的等比数列,
的等比数列,∵a2•a5=
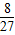 ,
,∴a1q•a1q4=
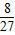 ,
,∴
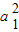 q5=
q5=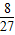 ,可得
,可得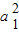 (
( )5=
)5=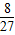 ,a1<0
,a1<0解得a1=-
 ,
,所以an=-(
 )n-2,
)n-2,故答案为:以an=-(
 )n-2
)n-2点评:本题考查数列与函数的关系,考查数列的通项与求和,确定数列是等比数列是关键,此题是一道基础题;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
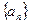 中,已知点
中,已知点 在
在 函数
函数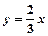 的图像上,且
的图像上,且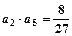 .
.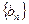 的前
的前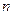 项和为
项和为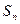 ,且
,且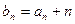 ,求
,求