题目内容
在各项均为负数的数列{an}中,已知点(an,an+1)(n∈N*)在函数y=| 2 |
| 3 |
| 8 |
| 27 |
(1)求证:数列{an}是等比数列,并求出其通项;
(2)若数列{bn}的前n项和为Sn,且bn=an+n,求Sn.
分析:(1)把点的坐标代入直线方程,根据等比数列的定义进行证明,显然公比是
,再根据条件a2•a5=
求出首项即可求出这个数列的通项公式;
(2)数列bn是一个等比数列和一个等差数列的对应项的和组成的数列,分别求和即可.
| 3 |
| 2 |
| 8 |
| 27 |
(2)数列bn是一个等比数列和一个等差数列的对应项的和组成的数列,分别求和即可.
解答:解:(1)因为点(an,an+1)(n∈N*)在函数y=
x的图象上,
所以an+1=
an,即
=
,故数列an是公比q=
的等比数列
因为a2a5=
,则a 1q•a1q4=
,即
(
)5=(
)3,由于数列an的各项均为负数,则a1=-
所以an=-(
)n-2.(6分)
(2)由(1)知,an=-(
)n-2,bn=-(
)n-2+n,
所以Sn=3•(
)n-1+
.(12分)
| 2 |
| 3 |
所以an+1=
| 2 |
| 3 |
| an+1 |
| an |
| 2 |
| 3 |
| 2 |
| 3 |
因为a2a5=
| 8 |
| 27 |
| 8 |
| 27 |
| a | 2 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
(2)由(1)知,an=-(
| 2 |
| 3 |
| 2 |
| 3 |
所以Sn=3•(
| 2 |
| 3 |
| n2+n-9 |
| 2 |
点评:本题考查等比数列的概念、通项,等比数列和等差数列的求和.高考对数列的考查难度在下降,其考查的重点转变为考查数列中的基本问题、两类基本数列,以及数列求和方面.解决两类基本数列问题的一个重要思想是基本量方法,即通过列出方程或者方程组求出等差数列的首项和公差、等比数列的首项和公比.数列求和要掌握好三个方法,一个是本题使用的分组求和,第二个是错位相减法,第三个是裂项求和法.

练习册系列答案
相关题目
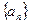 中,已知点
中,已知点 在
在 函数
函数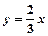 的图像上,且
的图像上,且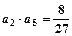 .
.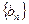 的前
的前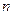 项和为
项和为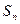 ,且
,且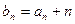 ,求
,求