题目内容
在各项均为负数的数列{an}中,已知2an=3an+1,且a2a5=
,
(1)求证:{an}是等比数列,并求出通项公式
(2)-
是这个数列的项吗?,如果是,是第几项?
| 8 |
| 27 |
(1)求证:{an}是等比数列,并求出通项公式
(2)-
| 16 |
| 81 |
分析:(1)根据题意,由2an=3an+1,可得
=
,由等比数列的定义,可得{an}是等比数列,同时可得{an}的公比,又由a2a5=
,可得a1的值,由等比数列的通项公式,可得答案,
(2)由(1)的结论,令-
=-(
)n-2,解可得n=6,为整数,可得结论.
| an+1 |
| an |
| 2 |
| 3 |
| 8 |
| 27 |
(2)由(1)的结论,令-
| 16 |
| 81 |
| 2 |
| 3 |
解答:解:(1)∵2an=3an+1,
∴
=
,故{an}是等比数列,且其公比为
,
又a1qa1q4=
得a12=
,(a1<0)即a1=-
所以,an=(-
)(
)n-1=-(
)n-2;
(2)由(1)的结论,令-
=-(
)n-2
得 (
)4=(
)n-2
由指数函数性质知4=n-2,即n=6,为正整数,
则-
是该数列的第6项.
∴
| an+1 |
| an |
| 2 |
| 3 |
| 2 |
| 3 |
又a1qa1q4=
| 8 |
| 27 |
| 9 |
| 4 |
| 3 |
| 2 |
所以,an=(-
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
(2)由(1)的结论,令-
| 16 |
| 81 |
| 2 |
| 3 |
得 (
| 2 |
| 3 |
| 2 |
| 3 |
由指数函数性质知4=n-2,即n=6,为正整数,
则-
| 16 |
| 81 |
点评:本题考查等比数列的判定与性质,解(1)时,注意根据题干条件“各项均为负数”,对求得的a1进行取舍.

练习册系列答案
相关题目
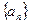 中,已知点
中,已知点 在
在 函数
函数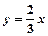 的图像上,且
的图像上,且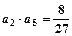 .
.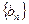 的前
的前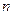 项和为
项和为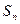 ,且
,且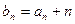 ,求
,求