题目内容
已知数列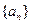 为等差数列,若
为等差数列,若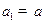
 ,
,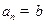 (
(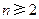 ,
,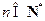 ),则
),则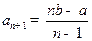 .
.
类比等差数列的上述结论,对等比数列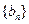 (
(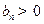 ,
,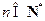 ),若
),若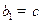 ,
,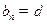
( ,
,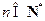 ),则可以得到
),则可以得到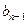 = .
= .
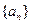 为等差数列,若
为等差数列,若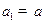
 ,
,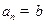 (
(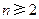 ,
,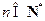 ),则
),则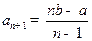 .
.类比等差数列的上述结论,对等比数列
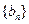 (
(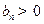 ,
,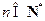 ),若
),若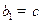 ,
,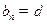
(
 ,
,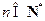 ),则可以得到
),则可以得到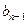 = .
= .
略

练习册系列答案
相关题目
题目内容
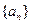 为等差数列,若
为等差数列,若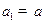
 ,
,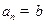 (
(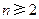 ,
,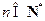 ),则
),则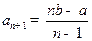 .
.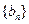 (
(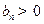 ,
,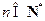 ),若
),若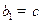 ,
,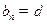
 ,
,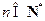 ),则可以得到
),则可以得到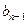 = .
= .
