题目内容
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且![]() .D为线段AC的中点.
.D为线段AC的中点.
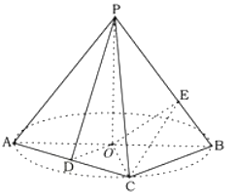
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点E在线段PB上,且![]() ,求三棱锥
,求三棱锥![]() 体积的最大值.
体积的最大值.
【答案】(1)证明见解析;(2)24.
【解析】
(1)由已知先证明AC⊥OD,又PO⊥AC,从而得到AC⊥平面PDO,进而证明平面PAC⊥平面PDO;
(2)由题意先求得△ABC面积的最大值,进而求得三棱锥PABC体积的最大值,从而求得三棱锥EPOC体积的最大值.
(1)证明:在ΔAOC中,因为OA=OC,D为AC的中点,所以AC⊥OD,
又PO垂直于圆O所在的平面,所以PO⊥AC;
又DO∩PO=O,所以AC⊥平面PDO;
又AC![]() 平面PAC,
平面PAC,
所以平面PAC⊥平面PDO;
(2)由PE=![]() PB,则
PB,则![]()
所以V三梭锥E-POC=V三棱锥C-POE=![]() V三棱维C-POB=
V三棱维C-POB=![]() S三棱维P-OCB=
S三棱维P-OCB=![]() V三棱维P-ACB
V三棱维P-ACB
又点C在圆O.上,所以当CO⊥AB时,C到AB的距离最大,且最大值为6;
又AB=12,所以ΔABC面积的最大值为![]() ×12×6=36;
×12×6=36;
又三棱锥P-ABC的高为PO=6,
所以三棱锥P-ABC体积的最大值为![]() ×36×6=72;
×36×6=72;

综上知,三棱锥E-POC体积的最大值为![]() ×72=24.
×72=24.

练习册系列答案
相关题目