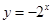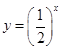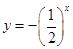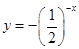题目内容
设函数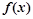 的定义域为D,若存在非零常数l使得对于任意
的定义域为D,若存在非零常数l使得对于任意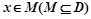 有
有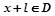 且
且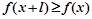 ,则称
,则称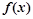 为M上的l高调函数.对于定义域为R的奇函数
为M上的l高调函数.对于定义域为R的奇函数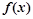 ,当
,当 ,若
,若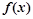 为R上的4高调函数,则实数a的取值范围为________
为R上的4高调函数,则实数a的取值范围为________
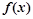 的定义域为D,若存在非零常数l使得对于任意
的定义域为D,若存在非零常数l使得对于任意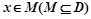 有
有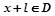 且
且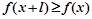 ,则称
,则称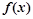 为M上的l高调函数.对于定义域为R的奇函数
为M上的l高调函数.对于定义域为R的奇函数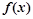 ,当
,当 ,若
,若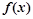 为R上的4高调函数,则实数a的取值范围为________
为R上的4高调函数,则实数a的取值范围为________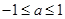
解:定义域为R的函数f(x)是奇函数,
当x≥0时,
f(x)=|x-a2|-a2,的图象如图,
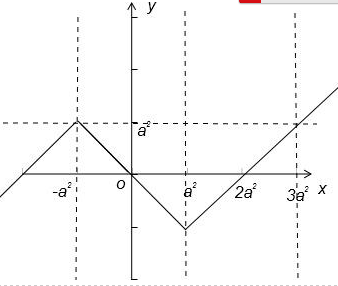
∵f(x)为R上的4高调函数,当x<0时,函数的最大值为a2,要满足f(x+l)≥f(x),4大于等于区间长度3a2-(-a2),
∴4≥3a2-(-a2),∴-1≤a≤1,
故选A.
当x≥0时,
f(x)=|x-a2|-a2,的图象如图,

∵f(x)为R上的4高调函数,当x<0时,函数的最大值为a2,要满足f(x+l)≥f(x),4大于等于区间长度3a2-(-a2),
∴4≥3a2-(-a2),∴-1≤a≤1,
故选A.

练习册系列答案
相关题目
 ,其中t是产品售出的数量,且
,其中t是产品售出的数量,且 (利润=销售收入
(利润=销售收入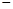 成本).
成本).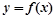 的解析式;
的解析式;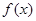 对任意
对任意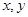 满足
满足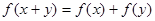 ,且
,且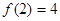 ,则
,则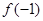 的值为
的值为 
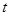 ,离开家里的路程为
,离开家里的路程为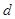 ,下面图象中,能反映该同学的情况的是( )
,下面图象中,能反映该同学的情况的是( )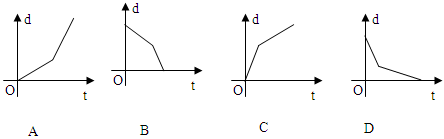
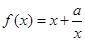 有如下性质:如果常数
有如下性质:如果常数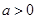 ,那么该函数在
,那么该函数在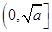 上是减函数,在
上是减函数,在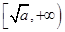 上是增函数.
上是增函数.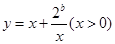 在
在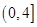 上是减函数,在
上是减函数,在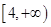 上是增函数,求
上是增函数,求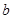 的值;
的值;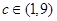 ,求函数
,求函数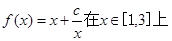 的最小值和最大值.
的最小值和最大值.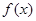 在
在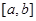 上有定义,若对任意
上有定义,若对任意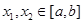 ,有
,有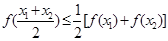
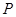 .设
.设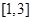 上的图像时连续不断的; ②
上的图像时连续不断的; ②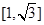 上具有性质
上具有性质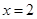 处取得最大值
处取得最大值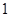 ,则
,则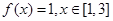 ;④对任意
;④对任意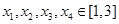 ,有
,有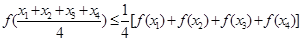
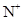 ,对应关系是:“取绝对值”.
,对应关系是:“取绝对值”.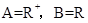 ,对应关系是:“求平方根”.
,对应关系是:“求平方根”. ,对应关系是:“平方加1”.
,对应关系是:“平方加1”.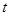 (天)的函数,且销售量近似满足函数
(天)的函数,且销售量近似满足函数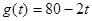 (件),价格近似满足函数
(件),价格近似满足函数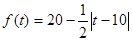 (元)。
(元)。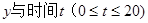 函数表达式;
函数表达式;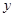 的最大值与最小值。
的最大值与最小值。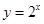 的图象关于原点对称的是( )
的图象关于原点对称的是( )