题目内容
如图,已知F1、F2分别为椭圆C1: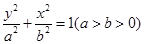 的上、下焦点,其中F1也是抛物线C2:
的上、下焦点,其中F1也是抛物线C2: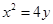 的焦点,点A是曲线C1,C2在第二象限的交点,且
的焦点,点A是曲线C1,C2在第二象限的交点,且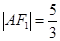

(Ⅰ)求椭圆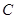 1的方程;
1的方程;
(Ⅱ)已知P是椭圆C1上的动点,MN是圆C: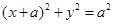 的直径,求
的直径,求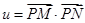 的最大值和最小值.
的最大值和最小值.
【答案】
(Ⅰ)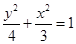 ;
;
(Ⅱ)当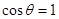 时,
时, ,当
,当 时,
时,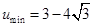 。
。
【解析】
试题分析:(Ⅰ)抛物线C2的焦点F1(0,1),准线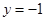 ,易得
,易得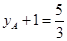 ∴
∴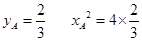
∴ 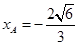 (正值舍去)∴
(正值舍去)∴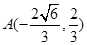 3分
3分
又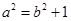 ………①
………① 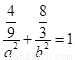 …………②
5分
…………②
5分
联立①②得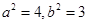 ∴椭圆C1的方程为
∴椭圆C1的方程为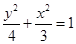 6分
6分
(Ⅱ)圆C: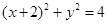 ∴圆心C(-2,0),半径
∴圆心C(-2,0),半径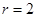
设P( )
7分
)
7分
法一: 9分
9分
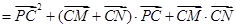
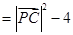
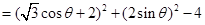
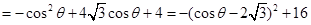 11分
11分
当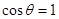 时,
时, 12分
12分
当 时,
时,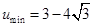 13分
13分
法二:设M( ),则N(
),则N(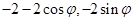 )
8分
)
8分
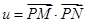
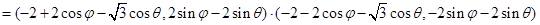
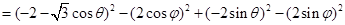
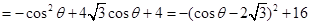 11分
11分
当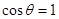 时,
时, 12分
12分
当 时,
时,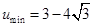 13分
13分
法三: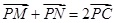 8分
8分
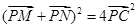
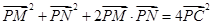
∵C是MN中点,∴ 9分
9分
∴ 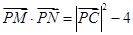 10分
10分
∴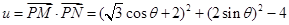
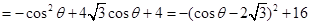 11分
11分
当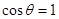 时,
时, 12分
12分
当 时,
时,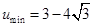 13分
13分
考点:本题主要考查抛物线的几何性质,椭圆的标准方程,椭圆的几何性质,直线椭圆的位置关系,平面向量的坐标运算。
点评:中档题,求椭圆的标准方程,主要运用了椭圆的几何性质,a,b,c,e的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)利用平面向量的坐标运算,将问题转化成三角函数问题,确定最值。

练习册系列答案
相关题目
 如图,已知F1、F2是椭圆
如图,已知F1、F2是椭圆 如图,已知F1,F2是椭圆C:
如图,已知F1,F2是椭圆C: (2012•鹰潭一模)如图,已知F1,F2是椭圆
(2012•鹰潭一模)如图,已知F1,F2是椭圆 如图,已知F1、F2分别为椭圆
如图,已知F1、F2分别为椭圆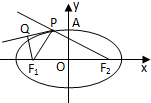 如图,已知F1、F2是椭圆
如图,已知F1、F2是椭圆