题目内容
【题目】已知抛物线C:y=x2 , 点P(0,2),A、B是抛物线上两个动点,点P到直线AB的距离为1.
(1)若直线AB的倾斜角为 ![]() ,求直线AB的方程;
,求直线AB的方程;
(2)求|AB|的最小值.
【答案】
(1)解:由直线AB的倾斜角为 ![]() ,tan
,tan ![]() =
= ![]() ,
,
设直线AB的方程为:y= ![]() x+m,
x+m,
则点P(0,2)到直线AB的距离为
d= 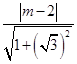 =1,
=1,
解得m=0或m=4;
∴直线AB的方程为y= ![]() x或y=
x或y= ![]() x+4
x+4
(2)解:设直线AB的方程为y=kx+m,
则点P到直线AB的距离为d= ![]() =1,
=1,
即k2+1=(m﹣2)2;
由 ![]() ,消去y得x2﹣kx﹣m=0,
,消去y得x2﹣kx﹣m=0,
由根与系数的关系得x1+x2=k,x1x2=﹣m;
∴|AB|2=(1+k2)[ ![]() ﹣4x1x2]=(1+k2)(k2+4m)=(m﹣2)2(m2+3),
﹣4x1x2]=(1+k2)(k2+4m)=(m﹣2)2(m2+3),
设f(m)=(m﹣2)2(m2+3),
则f′(m)=2(m﹣2)(2m2﹣2m+3),
又k2+1=(m﹣2)2≥1,
∴m≤1或m≥3,
∴当m∈(﹣∞,1]时,f′(m)<0,f(m)是单调减函数;
当m∈[3,+∞)时,f′(m)>0,f(m)是单调增函数;
∴f(m)min=f(1)=4,
∴|AB|的最小值为2
【解析】(1)由直线AB的倾斜角为 ![]() 设出直线AB的方程,
设出直线AB的方程,
根据点P到直线AB的距离求出m的值,从而写出直线方程;(2)设出直线AB的方程,与抛物线方程联立,
利用根与系数的关系和点P到直线AB的距离,
得出k、m的关系,再求|AB|2的最小值即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目