题目内容
【题目】已知 ![]() 是定义在
是定义在 ![]() 上的奇函数,当
上的奇函数,当 ![]() 时,
时, ![]() ,则不等式
,则不等式 ![]() 的解集为( )
的解集为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】∵f(x)是定义在[﹣4,4]上的奇函数,∴当x=0时,f(0)=0,
下面求x∈[﹣4,0)时的f(x)的表达式,设x∈[﹣4,0),则﹣x∈(0,4],
又∵当x>0时,f(x)=﹣x2+4x,∴f(﹣x)=﹣(﹣x)2+4(﹣x)=﹣x2﹣4x,
又f(x)是定义在[﹣4,4]上的奇函数,∴f(x)=﹣f(﹣x)=x2+4x,∴f(x)= ![]() ,
,
令f(x)=0,解得x=﹣4或0或4,当x∈[﹣4,0]时,不等式f[f(x)]<f(x),即(x2+4x)2+4(x2+4x)<x2+4x,化简得(x2+4x)2+3(x2+4x)<0,解得x∈(﹣4,﹣3)∪(﹣1,0);
当x∈(0,4]时,不等式f[f(x)]<f(x),即﹣(﹣x2+4x)2+4(﹣x2+4x)<﹣x2+4x,化简得﹣(﹣x2+4x)2+3(﹣x2+4x)<0,
解得x∈(1,3);综上所述,x∈(﹣4,﹣3)∪(﹣1,0)∪(1,3),故答案为:B.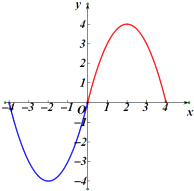
根据题意结合奇函数的定义对x分情况讨论解出在不同区间上的x的取值范围,最终把各种情况并起来即可。

【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 610 | ||
女大学生 | 90 | ||
合计 | 800 |
(1)根据题意完成表格;
(2)是否有95%的把握认为愿意做志愿者工作与性别有关? 参考公式及数据: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥K0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图.
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30] | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)估计这次学生参加社区服务人数的众数、中位数以及平均数.