题目内容
已知定点M(0,2),N(-2,0),直线l:kx-y-2k+2=0(k为常数).
(1)若点M,N到直线l的距离相等,求实数k的值;
(2)对于l上任意一点P,∠MPN恒为锐角,求实数k的取值范围.
(1)若点M,N到直线l的距离相等,求实数k的值;
(2)对于l上任意一点P,∠MPN恒为锐角,求实数k的取值范围.
(1)k=1或k=
(2)k∈(-∞,- )∪(1,+∞)
)∪(1,+∞)

(2)k∈(-∞,-
 )∪(1,+∞)
)∪(1,+∞)解:(1)∵点M、N到直线l的距离相等,
∴直线l平行于MN所在的直线或过MN的中点,
∴k=1或k= .
.
(2)设l上任意一点P(x0,kx0-2k+2).
若∠MPN恒为锐角,则 ·
· >0,
>0,
即(x0,kx0-2k)·(x0+2,kx0-2k+2)>0,
∴x02+2x0+(kx0-2k)2+2kx0-4k>0,
∴(1+k2)x02+(2k-4k2+2)x0+4k2-4k>0对x0∈R恒成立,
∴Δ=(2k-4k2+2)2-4(k2+1)(4k2-4k)<0,
即-7k2+6k+1<0,∴k>1或k<- ,
,
即k∈(-∞,- )∪(1,+∞).
)∪(1,+∞).
∴直线l平行于MN所在的直线或过MN的中点,
∴k=1或k=
 .
.(2)设l上任意一点P(x0,kx0-2k+2).
若∠MPN恒为锐角,则
 ·
· >0,
>0,即(x0,kx0-2k)·(x0+2,kx0-2k+2)>0,
∴x02+2x0+(kx0-2k)2+2kx0-4k>0,
∴(1+k2)x02+(2k-4k2+2)x0+4k2-4k>0对x0∈R恒成立,
∴Δ=(2k-4k2+2)2-4(k2+1)(4k2-4k)<0,
即-7k2+6k+1<0,∴k>1或k<-
 ,
,即k∈(-∞,-
 )∪(1,+∞).
)∪(1,+∞).
练习册系列答案
相关题目
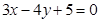 关于x轴对称的直线方程为( )
关于x轴对称的直线方程为( )


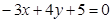

 的三个顶点是
的三个顶点是 求
求 边上的高所在直线的方程;
边上的高所在直线的方程; ,它们所表示的曲线可能是( )
,它们所表示的曲线可能是( )