题目内容
【题目】设数列![]() 对任意
对任意![]() 都有
都有![]() (其中
(其中![]() 、
、![]() 、
、![]() 是常数) .
是常数) .
(Ⅰ)当![]() ,
,![]() ,
,![]() 时,求
时,求![]() ;
;
(Ⅱ)当![]() ,
,![]() ,
,![]() 时,若
时,若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若数列![]() 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.当
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.当![]() ,
,![]() ,
,![]() 时,设
时,设![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() ,试问:是否存在这样的“封闭数列”,使得对任意
,试问:是否存在这样的“封闭数列”,使得对任意![]() ,都有
,都有![]() ,且
,且![]() .若存在,求数列
.若存在,求数列![]() 的首项
的首项![]() 的所有取值;若不存在,说明理由.
的所有取值;若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅱ)存在,
;(Ⅱ)存在,![]()
【解析】
(Ⅰ)当![]() ,
,![]() ,
,![]() 时,由已知条件推导出
时,由已知条件推导出![]() ,
,![]() ,由此得到数列
,由此得到数列![]() 是以首项为1,公比为3的等比数列,从而能求出
是以首项为1,公比为3的等比数列,从而能求出![]() ;
;
(Ⅱ)当![]() ,
,![]() ,
,![]() ,由已知条件推导出
,由已知条件推导出![]() ,从而得到数列
,从而得到数列![]() 是等差数列,由此求出
是等差数列,由此求出![]() ;
;
(Ⅲ)由(Ⅱ)知数列![]() 是等差数列,
是等差数列,![]() ,由此进行验证,求出数列
,由此进行验证,求出数列![]() 的首项
的首项![]() 的所有取值.
的所有取值.
(Ⅰ)当![]() ,
,![]() ,
,![]() 时,
时,![]()
![]() ①,用
①,用![]() 去换
去换
![]() 得
得![]()
![]() ②,②-①得,
②,②-①得,![]() ,即
,即![]() ,
,
在①中令![]() 得
得![]() ,故
,故![]() 是以1为首项,3为公比的等比数列,所以
是以1为首项,3为公比的等比数列,所以![]() ,
,
从而![]() .
.
(Ⅱ)当![]() ,
,![]() ,
,![]() 时,
时,![]()
![]() ③,用
③,用![]() 去换
去换![]() 得
得
![]()
![]() ④,④-③得,
④,④-③得,![]() ⑤,用
⑤,用
![]() 去换
去换![]() 得
得![]() ⑥,⑥-⑤得,
⑥,⑥-⑤得,![]() ,即
,即
![]() ,故
,故![]() 是等差数列,因为
是等差数列,因为![]() ,
,![]() ,所以公差
,所以公差![]() ,
,
故![]() .
.
(Ⅲ)由(Ⅱ)知![]() 是等差数列,因
是等差数列,因![]() ,所以
,所以![]() ,假设存在这样的“封闭数列”,
,假设存在这样的“封闭数列”,
则对任意![]() ,必存在
,必存在![]() ,使得
,使得![]()
![]()
![]() ,
,
所以![]() ,故
,故![]() 为偶数,
为偶数,![]() ,又由已知,
,又由已知,![]() ,
,
所以![]() ,此时
,此时![]() ;当
;当![]() 时,
时,![]() ,
,
![]() ,所以
,所以![]()
![]() ,
,
故![]()

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
【题目】某市组织高三全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如下:
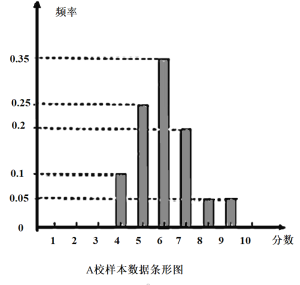
B校样本数据统计表:
成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(1)计算两校样本数据的均值和方差,并根据所得数据进行比较.
(2)从A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人,若从抽取的6人中任选2人参加更高一级的比赛,求这2人成绩之和大于或等于15的概率.