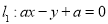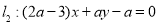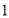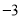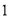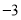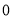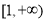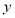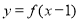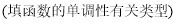题目内容
设定义域为 的函数
的函数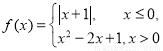
(Ⅰ)在平面直角坐标系内作出函数 的图象,并指出
的图象,并指出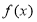 的单调区间(不需证明);
的单调区间(不需证明);
(Ⅱ)若方程 有两个解,求出
有两个解,求出 的取值范围(只需简单说明,不需严格证明).
的取值范围(只需简单说明,不需严格证明).
(Ⅲ)设定义为 的函数
的函数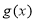 为奇函数,且当
为奇函数,且当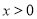 时,
时, 求
求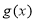 的解析式.
的解析式.

(Ⅰ)作图岁详解.单增区间: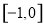 ,
,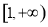 ,单减区间
,单减区间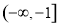 ,
,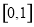 ;(Ⅱ)
;(Ⅱ)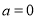 或
或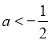 ;(Ⅲ)
;(Ⅲ) .
.
【解析】
试题分析:(Ⅰ)利用一次函数、二次函数的图象及对称性可作出图象,然后根据图象可写单调区间;(Ⅱ)考虑直线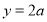 与函数
与函数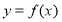 的图象只有两个交点时,写出
的图象只有两个交点时,写出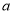 满足的条件;(Ⅲ)当
满足的条件;(Ⅲ)当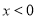 时,
时,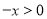 ,由此可得到
,由此可得到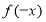 的解析式,然后利用函数奇偶性可求得
的解析式,然后利用函数奇偶性可求得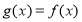 的解析式,又由奇函数的特性易知
的解析式,又由奇函数的特性易知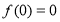 ,进而可求得
,进而可求得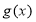 的解析式.
的解析式.
试题解析:(Ⅰ)如图.

单增区间: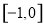 ,
,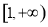 ,单减区间
,单减区间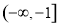 ,
,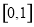 .
.
(Ⅱ)在同一坐标系中同时作出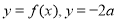 图象,由图可知
图象,由图可知 有两个解,
有两个解,
须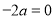 或
或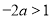 ,即
,即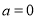 或
或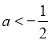 .
.
(Ⅲ)当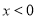 时,
时,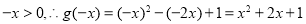 ,
,
因为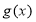 为奇函数,所以
为奇函数,所以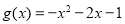 ,
,
且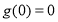 ,所以
,所以 .
.
考点:1、分段函数的图象;2、函数单调性及奇偶性.

练习册系列答案
相关题目