题目内容
函数 的定义域为
的定义域为 ,且对其内任意实数
,且对其内任意实数 均有:
均有: ,则
,则 在
在 上是
上是 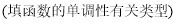
减函数
【解析】
试题分析:由题设对函数定义域 任意实数
任意实数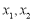 ,当
,当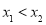 时,
时,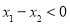 ,从而有
,从而有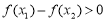 ,符合减函数的定义,故
,符合减函数的定义,故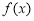 在
在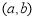 上是减函数.
上是减函数.
考点:函数单调性的定义

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
函数 的定义域为
的定义域为 ,且对其内任意实数
,且对其内任意实数 均有:
均有: ,则
,则 在
在 上是
上是 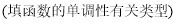
减函数
【解析】
试题分析:由题设对函数定义域 任意实数
任意实数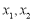 ,当
,当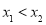 时,
时,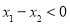 ,从而有
,从而有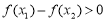 ,符合减函数的定义,故
,符合减函数的定义,故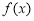 在
在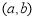 上是减函数.
上是减函数.
考点:函数单调性的定义

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案