题目内容
19.直线l与曲线C:y=x2+3相交于A,B,且线段AB的中点为P(-1,5),求直线l的方程.分析 设A(x1,y1),B(x2,y2),代入抛物线的方程,相减再运用平方差公式和直线的斜率公式及中点坐标公式,即可得到斜率,再由点斜式方程,即可得到所求直线方程.
解答 解:设A(x1,y1),B(x2,y2),
即有y1=x12+3,y2=x22+3,
相减可得y1-y2=(x1-x2)(x1+x2),
kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=x1+x2,
由线段AB的中点为P(-1,5),
可得x1+x2=-2,则kAB=-2,
即有直线AB的方程为y-5=-2(x+1),
即为y=-2x+3.
点评 本题考查直线方程的求法,注意运用点差法,及中点坐标公式和直线的斜率公式,属于基础题.

练习册系列答案
相关题目
4.已知点A(1,-2,2),B(2,-2,1),C(6,5,2),O为坐标原点,则三棱锥O-ABC的体积为( )
| A. | $\frac{65}{3}$ | B. | $\frac{\sqrt{65}}{3}$ | C. | $\frac{31}{6}$ | D. | $\frac{65}{6}$ |
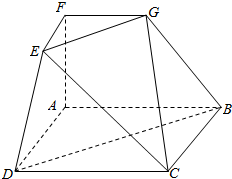 如图,在几何体ABCD-EFG中,下地面ABCD为正方形,上底面EFG为等腰直角三角形,其中EF⊥FG,且EF∥AD,FG∥AB,AF⊥面ABCD,AB=2FG=2,BE=BD,M是DE的中点.
如图,在几何体ABCD-EFG中,下地面ABCD为正方形,上底面EFG为等腰直角三角形,其中EF⊥FG,且EF∥AD,FG∥AB,AF⊥面ABCD,AB=2FG=2,BE=BD,M是DE的中点.