题目内容
9.已知数列{an}的首项a1=1,a2=3,前n项和为Sn且$\frac{{S}_{n+1}-{S}_{n}}{{S}_{n}-{S}_{n-1}}=\frac{{2a}_{n}+1}{{a}_{n}}$,(n≥2,n∈N*)设b1=1,bn+1=log2(an+1)+bn(n∈N*)(1)设cn=$\frac{{4}^{\frac{{b}_{n+1}-1}{n+1}}}{{a}_{n}{a}_{n+1}}$,记Gn=$\sum_{k=1}^{n}{c}_{k}$,试比较Gn与1的大小,并说明理由;
(2)若数列{ln}满足ln=log2(an+1)(n∈N*),在每两个lk与lk+1之间都插入2k-1(k=1,2,3,…,k∈N*)个2,使得数列{ln}变成了一个新的数列{tp},试问:是否存在正整数m,使得数列{tp}的前m项的和Tm=2015?如果存在,求出m的值:如果不存在,说明理由.
分析 (1)由$\frac{{S}_{n+1}-{S}_{n}}{{S}_{n}-{S}_{n-1}}=\frac{{2a}_{n}+1}{{a}_{n}}$,(n≥2,n∈N*),可得$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{2{a}_{n}+1}{{a}_{n}}$,化为an+1=2an+1,变形为an+1+1=2(an+1),利用等比数列的通项公式即可得出an.
bn+1=log2(an+1)+bn=n+bn,可得bn+1-bn=n,利用“累加求和”即可得出bn.可得cn=$\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1}$,利用“裂项求和”可得Gn.
(2)ln=log2(an+1)=n.假设存在正整数m,使得数列{tp}的前m项的和Tm=2015.数列{tp}:1;2,2;2,2,3;2,2,2,2,4;…,k;$\underset{\underbrace{2,2,…,2}}{{2}^{k-1}}$,k+1;….T521=${T}_{{2}^{9}-1+10}$=1077<2015,2015-1077=938=2×469,进而得出.
解答 解:(1)由$\frac{{S}_{n+1}-{S}_{n}}{{S}_{n}-{S}_{n-1}}=\frac{{2a}_{n}+1}{{a}_{n}}$,(n≥2,n∈N*),可得$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{2{a}_{n}+1}{{a}_{n}}$,化为an+1=2an+1,
变形为an+1+1=2(an+1),
又数列{an}的首项a1=1,a2=3,
当n=1时也满足,
因此数列{an+1}是等比数列,首项为2,公比为2,∴an+1=2•2n-1,∴an=2n-1.
bn+1=log2(an+1)+bn=n+bn,
∴bn+1-bn=n,
∴bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=(n-1)+(n-2)+…+1+1
=$\frac{n(n-1)}{2}$+1.
$\frac{{b}_{n+1}-1}{n+1}$=$\frac{\frac{n(n+1)}{2}+1-1}{n+1}$=$\frac{n}{2}$.
cn=$\frac{{4}^{\frac{{b}_{n+1}-1}{n+1}}}{{a}_{n}{a}_{n+1}}$=$\frac{{2}^{n}}{({2}^{n}-1)({2}^{n+1}-1)}$=$\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1}$,
Gn=$\sum_{k=1}^{n}{c}_{k}$=$(\frac{1}{2-1}-\frac{1}{{2}^{2}-1})$+$(\frac{1}{{2}^{2}-1}-\frac{1}{{2}^{3}-1})$+…+$(\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1})$=1-$\frac{1}{{2}^{n+1}-1}$<1.
∴Gn<1.
(2)ln=log2(an+1)=n.
假设存在正整数m,使得数列{tp}的前m项的和Tm=2015.
数列{tp}:1;2,2;2,2,3;2,2,2,2,4;…,k;$\underset{\underbrace{2,2,…,2}}{{2}^{k-1}}$,k+1;….
T521=${T}_{{2}^{9}-1+10}$=1+2+2+(2+2)+3+22×2+4+…+9+28×2+10=(1+2+…+10)+(2+22+…+29)=$\frac{10×11}{2}$+$\frac{2({2}^{9}-1)}{2-1}$=1077<2015,
2015-1077=938=2×469,
T990=T521+469=1+2+2+(2+2)+3+22×2+4+…+9+28×2+10+2+2+…+2=2015,
因此存在正整数m=990,使得数列{tp}的前990项的和Tm=2015.
点评 本题考查了递推关系的应用、等比数列的通项公式与前n项和公式、“裂项求和”方法、“累加求和”方法,考查了推理能力与计算能力,属于难题.

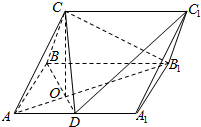 在侧面ABB1A1为长方形的三棱柱ABC-A1B1C1中,AB=a,AA1=$\sqrt{2}$a,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,且OC=OA.
在侧面ABB1A1为长方形的三棱柱ABC-A1B1C1中,AB=a,AA1=$\sqrt{2}$a,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,且OC=OA.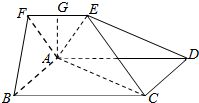 如图,在五面体ABCDEF中,四边形ABCD是边长为4的正方形,EF∥AD,
如图,在五面体ABCDEF中,四边形ABCD是边长为4的正方形,EF∥AD,