题目内容
8.在平面直角坐标系中,O为坐标原点,A(1,2),B(7,5),C在线段AB上,且满足2|AC|=|BC|,则|OC|的长等于3$\sqrt{2}$.分析 由已知条件利用定比分点公式求出C点坐标,由此能求出|OC|的长.
解答 解:设C(x,y),
∵在平面直角坐标系中,O为坐标原点,A(1,2),B(7,5),C在线段AB上,且满足2|AC|=|BC|,
∴$\left\{\begin{array}{l}{x=\frac{1+\frac{1}{2}×7}{1+\frac{1}{2}}}\\{y=\frac{2+\frac{1}{2}×5}{1+\frac{1}{2}}}\end{array}\right.$,即$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,
∴|OC|=$\sqrt{9+9}$=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 本题考查线段长的求法,是基础题,解题时要认真审题,注意定比分点公式的合理运用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
18.如图,在复平面内,复数z1和z2对应的点分别是A和B,则$\frac{{z}_{2}}{{z}_{1}}$=( )
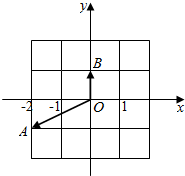

| A. | $\frac{1}{5}$+$\frac{2}{5}$i | B. | $\frac{2}{5}$+$\frac{1}{5}$i | C. | -$\frac{1}{5}$-$\frac{2}{5}$i | D. | -$\frac{2}{5}$-$\frac{1}{5}$i |
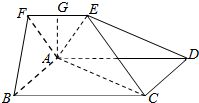 如图,在五面体ABCDEF中,四边形ABCD是边长为4的正方形,EF∥AD,
如图,在五面体ABCDEF中,四边形ABCD是边长为4的正方形,EF∥AD,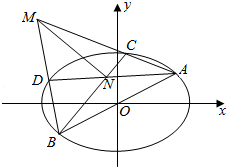 如图,在平面直角坐标系xoy中,椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,AB=$4\sqrt{5}$,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.
如图,在平面直角坐标系xoy中,椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,AB=$4\sqrt{5}$,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N. 直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1点的中点,且AA1=AC=BC=$\frac{\sqrt{2}}{2}$AB.
直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1点的中点,且AA1=AC=BC=$\frac{\sqrt{2}}{2}$AB.