题目内容
【题目】已知函数f(x)=Asin(ωx+α)(A>0,ω>0,﹣ ![]() <α<
<α< ![]() )的最小正周期是π,且当x=
)的最小正周期是π,且当x= ![]() 时,f(x)取得最大值2.
时,f(x)取得最大值2.
(1)求f(x)的解析式,并作出f(x)在[0,π]上的图象(要列表);
(2)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
【答案】
(1)解:因为函数f(x)的最小正周期是π,所以ω=2.
又因为 ![]() 时,f(x)取得最大值2.所以A=2,
时,f(x)取得最大值2.所以A=2,
同时 ![]() ,
, ![]() ,∵
,∵ ![]() ∴
∴ ![]() ,
,
∴函数y=f(x)的解析式 ![]() .
.
∵x∈[0,π],∴ ![]() ,列表如下:
,列表如下:
|
|
| π |
| 2π |
|
x | 0 |
|
|
|
| x |
f(x) | 1 | 2 | 0 | ﹣2 | 0 | 1 |
描点、连线得下图
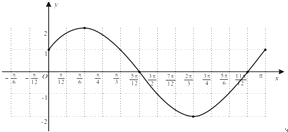
(2)解:由已知得y=g(x)=f(x﹣m)= ![]() 是偶函数,
是偶函数,
所以 ![]() ,
, ![]() ,
,
又因为m>0,所以m的最小值为 ![]()
【解析】(1)由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,用五点法作函数y=Asin(ωx+φ)在一个周期上的图象.(2)利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的奇偶性,求得m的最小值.
【考点精析】本题主要考查了五点法作函数y=Asin(ωx+φ)的图象和函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线);图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.

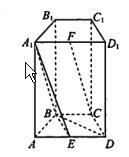
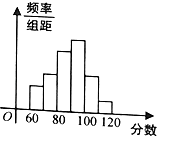
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).

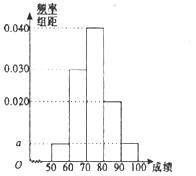
(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式: 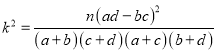 ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |