Question

【题目】已知f（α）= ．
（1）若α为第二象限角且f（α）=﹣ ，求 的值；
（2）若5f（α）=4f（3α+2β）．试问tan（2α+β）tan（α+β）是否为定值（其中α≠kπ+ ，α+β≠kπ+ ，2α+β≠kπ+ ，3α+2β≠kπ+ ，k∈Z）？若是，请求出定值；否则，说明理由．

Answer 1

【答案】
（1）解：f（α）= =

，α为第二象限角，得 ．

=

=

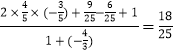
（2）解：∵5f（α）=4f（3α+2β），

∴5cos[（2α+β）﹣（α+β）]=4cos[（2α+β）+（α+β）]．

可得：5[cos（2α+β）cos（α+β）+sin（2α+β）sin（α+β）]

=4[cos（2α+β）cos（α+β）﹣sin（2α+β）sin（α+β）]，

化简：cos（2α+β）cos（α+β）=﹣9sin（2α+β）sin（α+β）．

又

知cos（2α+β）cos（α+β）≠0

故tan（2α+β）tan（α+β）= ．

综上tan（2α+β）tan（α+β）是定值

【解析】（1）直接化简f（α）=cosα，由α为第二象限角求出sinα，再由二倍角公式化简计算得答案；（2）由5f（α）=4f（3α+2β），得5cos[（2α+β）﹣（α+β）]=4cos[（2α+β）+（α+β）]，进一步化简可得cos（2α+β）cos（α+β）=﹣9sin（2α+β）sin（α+β），由已知条件可得cos（2α+β）cos（α+β）≠0，即可求出答案．