题目内容
若从集合{-1,1,2,3}中随机取出一个数m,放回后再随机取出一个数n,则使方程
+
=1表示焦点在x轴上的椭圆的概率为
.
| x2 |
| m2 |
| y2 |
| n2 |
| 5 |
| 16 |
| 5 |
| 16 |
分析:根据焦点位于x轴上的椭圆,则m2>n2,根据m2>n2,对A中元素进行分析可得到表示焦点在x轴上的椭圆共有多少个,根据概率公式计算即可得出答案.
解答:解:从集合{-1,1,2,3}中随机取出一个数m,放回后再随机取出一个数n,
所有的选法有:4×4=16,
焦点位于x轴上的椭圆,则m2>n2
当m=3时,n=-1,1,2;
当m=2时,n=-1,1;
方程
+
=1表示焦点在x轴上的椭圆共有5个,
方程表示焦点在x轴上的椭圆的概率是
;
故答案为:
.
所有的选法有:4×4=16,
焦点位于x轴上的椭圆,则m2>n2
当m=3时,n=-1,1,2;
当m=2时,n=-1,1;
方程
| x2 |
| m2 |
| y2 |
| n2 |
方程表示焦点在x轴上的椭圆的概率是
| 5 |
| 16 |
故答案为:
| 5 |
| 16 |
点评:本题主要考查椭圆的标准形式、等可能事件的概率,此题的关键是根据条件得出m2>n2.属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
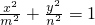 表示焦点在x轴上的椭圆的概率为________.
表示焦点在x轴上的椭圆的概率为________.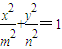 表示焦点在x轴上的椭圆的概率为 .
表示焦点在x轴上的椭圆的概率为 .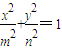 表示焦点在x轴上的椭圆的概率为 .
表示焦点在x轴上的椭圆的概率为 .