题目内容
从集合{-1,1,2,3}中任意取出两个不同的数记作m,n,则方程
+
=1表示焦点在x轴上的双曲线的概率是
.
| x2 |
| m |
| y2 |
| n |
| 1 |
| 4 |
| 1 |
| 4 |
分析:依据焦点在x轴上的双曲线判断出m>0,n<0,用古典摡型概率公式即可.
解答:解:焦点在x轴上的双曲线
则m>0,n<0
所以n=-1,适合题意的有3种,
从集合{-1,1,2,3}中任意取出两个不同的数记作m,n,共有A42=12种取法,
焦点在x轴上的双曲线的概率是:
=
故答案为
.
则m>0,n<0
所以n=-1,适合题意的有3种,
从集合{-1,1,2,3}中任意取出两个不同的数记作m,n,共有A42=12种取法,
焦点在x轴上的双曲线的概率是:
| 3 |
| 12 |
| 1 |
| 4 |
故答案为
| 1 |
| 4 |
点评:本题主要考查了双曲线的基本性质、排列、组合及简单计数问题等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
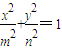 表示焦点在x轴上的椭圆的概率为 .
表示焦点在x轴上的椭圆的概率为 .