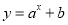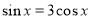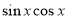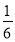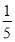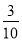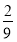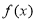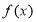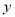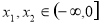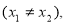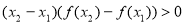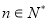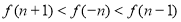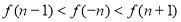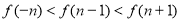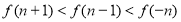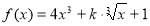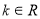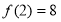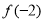题目内容
设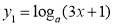 ,
,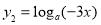 ,其中
,其中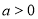 且
且 .
.
(I) 若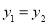 ,求
,求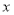 的值; (II) 若
的值; (II) 若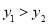 ,求
,求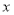 的取值范围.
的取值范围.
(I)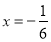 (II)当
(II)当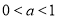 时,
时,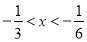 ;当
;当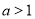 时,
时,
【解析】
试题分析:(I)底数相同时,两对数相等则真数相等。(II)应先讨论单调性,再用单调性解不等式,应注意真数大于0。由以上条件得到的不等式组即可求 的取值范围。
的取值范围。
试题解析:解:(1)
 ,即
,即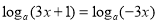 ∴
∴ ,
,
解得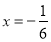 ,
,
检验 ,所以
,所以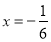 是所求的值。 5分
是所求的值。 5分
(2)当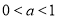 时,
时,
 ,即
,即
∴ 解得
解得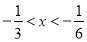 , 8分
, 8分
当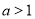 时,
时,
 ,即
,即
∴ 解得
解得 , 11分
, 11分
综上,当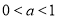 时,
时,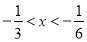 ;当
;当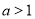 时,
时, 12分
12分
考点:对数的单调性。

练习册系列答案
相关题目