题目内容
【题目】如图,正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB.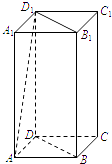
(1)求AD1与面BB1D1D所成角的正弦值;
(2)点E在侧棱AA1上,若二面角E﹣BD﹣C1的余弦值为 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:以D为原点,DA,DC,DD1分别为x轴,y轴,z轴,建立如图所示空间直角坐标系D﹣xyz.
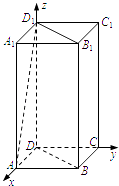
设AB=1,则D(0,0,0),A(1,0,0),
B(1,1,0),C(0,1,0),D1(0,0,2),
A1(1,0,2),B1(1,1,2),C1(0,1,2).
设AD1与面BB1D1D所成角的大小为θ, ![]() ,
,
设平面BB1D1D的法向量为 ![]() =(x,y,z),
=(x,y,z), ![]() ,
, ![]() ,
,
则 ![]() =0,
=0, ![]() ,即x+y=0,z=0.
,即x+y=0,z=0.
令x=1,则y=﹣1,所以n=(1,﹣1,0),
sinθ=|cos< ![]() >|=
>|= 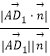 =
= ![]() ,
,
所以AD1与平面BB1D1D所成角的正弦值为 ![]()
(2)解:设E(1,0,λ),0≤λ≤2.
设平面EBD的法向量为 ![]() =(x1,y1,z1),平面BDC1的法向量为
=(x1,y1,z1),平面BDC1的法向量为 ![]() =(x2,y2,z2),
=(x2,y2,z2), ![]() ,
,
由 ![]() ,
, ![]() ,得x1+y1=0,x1+λz1=0,
,得x1+y1=0,x1+λz1=0,
令z1=1,则x1=﹣λ,y1=λ,n1=(﹣λ,λ,1), ![]() ,
,
由 ![]() ,
, ![]() ,得x2+y2=0,y2+2z2=0,
,得x2+y2=0,y2+2z2=0,
令z2=1,则x2=2,y2=﹣2,n2=(2,﹣2,1),
cos< ![]() >=
>= ![]() =
= ![]() ,
,
所以 ![]() ,得λ=1.
,得λ=1.
所以 ![]() =
= ![]() .
.
【解析】(1)建立空间直角坐标系,求出平面的法向量,利用向量法即可求AD1与面BB1D1D所成角的正弦值;(2)求出平面的法向量,根据二面角与平面法向量之间的关系进行求解即可.
【考点精析】掌握空间角的异面直线所成的角是解答本题的根本,需要知道已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则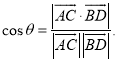 .
.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案