题目内容
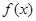 是奇函数,则①
是奇函数,则①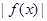 一定是偶函数;②
一定是偶函数;②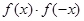 一定是偶函数;③
一定是偶函数;③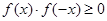 ;④
;④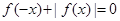 ,其中错误的个数有( )
,其中错误的个数有( )| A.1个 | B.2个 | C.4个 | D.0个 |
B
分析:由题意可得f(-x)=-f(x)
①|f(-x)|=|-f(x)|=|f(x)|是偶函数;
②令g(x)=f(x)?f(-x),则g(-x)=f(-x)?f(x)=g(x)是偶函数;
③f(x)?f(-x)=-f2(x)≤0;
④f(-x)+|f(x)|=|f(x)|-f(x)=0不一定成立
解答:解:∵f(x)是奇函数,
∴f(-x)=-f(x)
①|f(-x)|=|-f(x)|=|f(x)|是偶函数;故①正确
②令g(x)=f(x)?f(-x),则g(-x)=f(-x)?f(x)=g(x)是偶函数;故②正确
③由奇函数的性质可知,f(x)?f(-x)=-f2(x)≤0;故③错误
④f(-x)+|f(x)|=|f(x)|-f(x)=0不一定成立;故④错误
其中错误的有③④
故选B
①|f(-x)|=|-f(x)|=|f(x)|是偶函数;
②令g(x)=f(x)?f(-x),则g(-x)=f(-x)?f(x)=g(x)是偶函数;
③f(x)?f(-x)=-f2(x)≤0;
④f(-x)+|f(x)|=|f(x)|-f(x)=0不一定成立
解答:解:∵f(x)是奇函数,
∴f(-x)=-f(x)
①|f(-x)|=|-f(x)|=|f(x)|是偶函数;故①正确
②令g(x)=f(x)?f(-x),则g(-x)=f(-x)?f(x)=g(x)是偶函数;故②正确
③由奇函数的性质可知,f(x)?f(-x)=-f2(x)≤0;故③错误
④f(-x)+|f(x)|=|f(x)|-f(x)=0不一定成立;故④错误
其中错误的有③④
故选B

练习册系列答案
相关题目
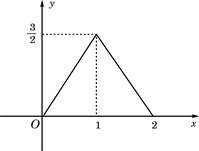
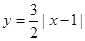 (0≤x≤2)
(0≤x≤2)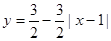 (0≤x≤2)
(0≤x≤2)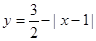 (0≤x≤2)
(0≤x≤2)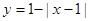 (0≤x≤2)
(0≤x≤2)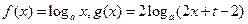
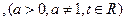 .
.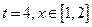 ,且
,且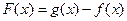 有最小值2
有最小值2 时,求
时,求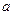 的值;
的值;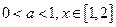 时,有
时,有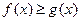 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.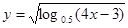 的定义域是 ( )
的定义域是 ( )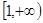
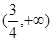
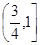
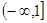
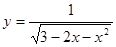 的定义域为( )
的定义域为( )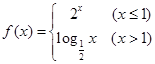 ,则函数
,则函数 的图象是 ( )
的图象是 ( )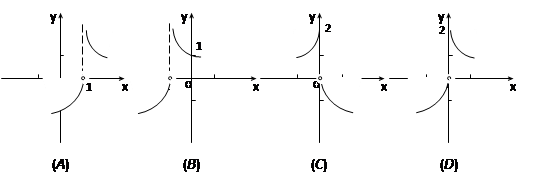
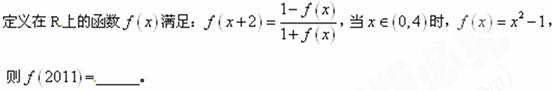
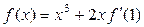 ,则
,则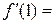 .
.