题目内容
有6名乒乓球运动员分别来自3个不同国家，每一个国家2人，他们排成一排，列队上场，要求同一国家的人不能相邻，那么不同的排法有 （ ）
| A．720种 | B．432种 | C．360种 | D．240种 |
D
不相邻问题用插空解题法：
假设6名运动员分别来自A,B,C三个国家，让A国的排队，有2种排法。此时：（）0（）0（）这两名运动员间有3个空位。0表示A国运动员的位置。
再从这3个空位中选两个给B国的运动员排，有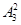
种排法。此时：（）0（）0（）0（）0（）四名运动员间有5个空位。
从这5个空位中选两个给C国的运动员排队，有
种排法。
所以总共有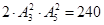
种排法，故选D
假设6名运动员分别来自A,B,C三个国家，让A国的排队，有2种排法。此时：（）0（）0（）这两名运动员间有3个空位。0表示A国运动员的位置。
再从这3个空位中选两个给B国的运动员排，有
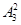种排法。此时：（）0（）0（）0（）0（）四名运动员间有5个空位。从这5个空位中选两个给C国的运动员排队，有
种排法。所以总共有
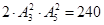种排法，故选D
练习册系列答案
相关题目
的项的系数是
。
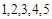五个数字组成无重复数字的五位数，按从小到大的顺序排成一个数列，则32154是第（ ）个数
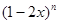的展开式中，各项的二项式系数之和是64，则
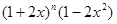的展开式中，
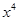项的系数是_________