题目内容
16.若f(x)是定义在R上的奇函数,且对任意的实数x≥0,总有正常数T,使得f(x+T)=f(x)+T成立,则称f(x)具有“性质p”,已知函数g(x)具有“性质p”,且在[0,T]上,g(x)=x2;若当x∈[-T,4T]时,函数y=g(x)-kx恰有8个零点,则实数k=4$\sqrt{3}$-6.分析 由题意可得g(T)=g(0)+T,从而求出T,再作函数y=g(x)与y=kx在[-1,4]上的图象,由数形结合求解即可.
解答 解:∵g(T)=g(0)+T,
∴T2=0+T,
解得,T=1或T=0(舍去);
故作函数y=g(x)与y=kx在[-1,4]上的图象如下,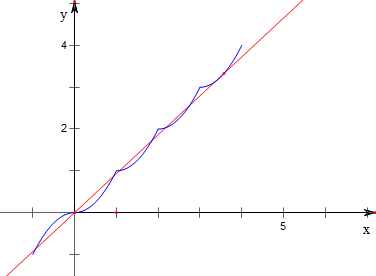
结合图象可知,
当直线y=kx与y=g(x)在最后一段上相切时,有8个交点,
即函数y=g(x)-kx恰有8个零点;
此时设切点为(x1,g(x1)),则
$\frac{g({x}_{1})}{{x}_{1}}$=g′(x1),
即$\frac{({x}_{1}-3)^{2}+3}{{x}_{1}}$=2(x1-3),
解得,x1=2$\sqrt{3}$,
故k=2(2$\sqrt{3}$-3)=4$\sqrt{3}$-6.
故答案为:4$\sqrt{3}$-6.
点评 本题考查了数形结合的思想应用及导数的综合应用,属于中档题.

练习册系列答案
相关题目
11.已知f(x)=Asin(wx+θ),(w>0),若两个不等的实数x1,x2∈$\left\{{x\left|{f(x)=\frac{A}{2}}\right.}\right\}$,且|x1-x2|min=π,则f(x)的最小正周期是( )
| A. | 3π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
8.复数z满足z(1-i)=2(i是虚数单位),则z=( )
| A. | 1+i | B. | -1+i | C. | -1-i | D. | 1-i |
 如图,在直三角形ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形
如图,在直三角形ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形 四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD中点,PA=2AB=2.
四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD中点,PA=2AB=2. 如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π]),OP所经过正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论:
如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π]),OP所经过正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论: