题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 是椭圆的两个焦点,
是椭圆的两个焦点,![]() 是椭圆上任意一点,且
是椭圆上任意一点,且![]() 的周长是6.
的周长是6.
(1)求椭圆![]() 的方程;
的方程;
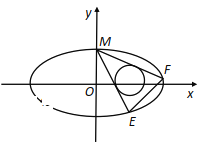
(2)设圆:![]() ,过椭圆的上顶点作圆
,过椭圆的上顶点作圆![]() 的两条切线交椭圆于
的两条切线交椭圆于![]() 两点,当圆心在
两点,当圆心在![]() 轴上移动且
轴上移动且![]() 时,求
时,求![]() 的斜率的取值范围.
的斜率的取值范围.

【答案】(1)![]() .
.
(2)![]() .
.
【解析】
(1)由椭圆离心率得到![]() 的关系,再由
的关系,再由![]() 的周长是
的周长是![]() ,得
,得![]() 的另一关系,联立求得
的另一关系,联立求得![]() 的值,代入
的值,代入![]() 求得
求得![]() ,则椭圆方程可求;(2)椭圆的上顶点为
,则椭圆方程可求;(2)椭圆的上顶点为![]() ,设过点
,设过点![]() 与圆
与圆![]() 相切的直线方程为
相切的直线方程为![]() ,由圆心到切线距离等于半径得到关于切线斜率的方程,由根与系数关系得到
,由圆心到切线距离等于半径得到关于切线斜率的方程,由根与系数关系得到![]() ,
,![]() ,再联立切线方程和椭圆方程,求得
,再联立切线方程和椭圆方程,求得![]() 的坐标,同理求得
的坐标,同理求得![]() 坐标,利用斜率公式得到
坐标,利用斜率公式得到![]() ,然后由函数单调性求得
,然后由函数单调性求得![]() 的斜率的范围.
的斜率的范围.
(1)由![]() ,可知
,可知![]() ,
,
因为![]() 的周长是6,所以
的周长是6,所以![]() ,
,
所以![]() ,所求椭圆方程为
,所求椭圆方程为![]() ;
;
(2)椭圆的上顶点为![]() ,设过点
,设过点![]() 与圆
与圆![]() 相切的直线方程为
相切的直线方程为![]() ,
,
由直线![]() 与
与![]() 相切可知
相切可知![]() ,
,
∴![]() ,
,
由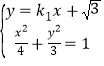 得
得![]() ,
,
∴![]() ,同理
,同理![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 为增函数,故
为增函数,故![]() 的斜率的范围为
的斜率的范围为![]() .
.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(I)试根据上述数据完成![]() 列联表:
列联表:

(II)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ,其中
,其中![]() .
.
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() ,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型,求y关于x的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为![]() =0.06e0.2303x,且相关指数R2=0.9522.
=0.06e0.2303x,且相关指数R2=0.9522.
( i )试与(Ⅰ)中的回归模型相比,用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为

![]() =
=![]()
![]() ;相关指数R2=
;相关指数R2= .
.


