题目内容
【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计，随机抽取了
名学生作为样本，得到这
名学生参加社区服务的次数，根据此数据作出了频率分布统计表和频率分布直方图如下：
（1）求表中
的值和频率分布直方图中
的值，并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数；
（2）如果用分层抽样的方法从样本服务次数在
和
的人中共抽取6人，再从这6人中选2人，求2人服务次数都在的概率.
【答案】（1）
,
，中位数为
；（2）
【解析】
试题分析：（1）由第一组内频数为
，频率为
可求出总人数为
，由此可求出第二组的频率为
，并可求频率直方图中
，由频率之和为
可求出
，频率分布直方图求出面积的一半处求出中位数即可；（2）分分层抽样的原则先求出共抽取
人时在
和
的人数，再列出所有基本事件，可求2人服务次数都在的概率.
试题解析：（1）因
，所以
，所以，
，
.
中位数位于区间
，设中位数为
，
则
，所以
，所以学生参加社区服务区次数的中位数为17次.
（2）由题意知样本服务次数在
有20人，样本服务次数在
有4人，
如果用分层抽样的方法从样本服务次数在和的人中共抽取6人，则抽取的服务次数在和的人数分别为：
和
.
记服务次数在为
，在的为
.
从已抽取的6人任选两人的所有可能为：
共15种，
设“2人服务次数都在”为事件
，则事件
包括
共10种，
所有
.
【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A，B两种不同的教学方式分别在甲、乙两个班进行教改实验．为了了解教学效果，期末考试后，陈老师对甲、乙两个班级的学生成绩进行统计分析，画出频率分布直方图(如下图)．记成绩不低于90分者为“成绩优秀”．
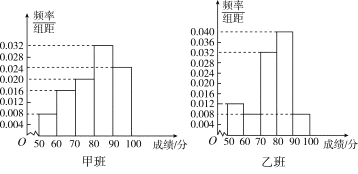
（Ⅰ）根据频率分布直方图填写下面2×2列联表；
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
（Ⅱ）判断能否在犯错误的概率不超过0.05的前提下认为：“成绩优秀”与教学方式有关？
附：
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
