题目内容
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() ,
, ![]() ,且
,且![]() ,记动点
,记动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 方程;
方程;
(Ⅱ)过点![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 相交
相交![]() 两点,试问在
两点,试问在![]() 轴上是否存在与点
轴上是否存在与点![]() 不同的定点
不同的定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]()
【解析】试题分析:(Ⅰ)由![]() ,
, ![]() ,且
,且![]() ,结合椭圆的定义即可求出曲线
,结合椭圆的定义即可求出曲线![]() 方程;(Ⅱ)当直线
方程;(Ⅱ)当直线![]() 与
与![]() 轴垂直时,求出
轴垂直时,求出![]() 的坐标,然后再证明对任意的直线
的坐标,然后再证明对任意的直线![]() ,均有
,均有![]() ,考虑直线斜率是否存在,然后联立直线与椭圆方程,结合韦达定理即可证明.
,考虑直线斜率是否存在,然后联立直线与椭圆方程,结合韦达定理即可证明.
试题解析:(1)∵![]() ,
, ![]() ,且
,且![]()
∴动点![]() 的轨迹为椭圆,即椭圆方程为
的轨迹为椭圆,即椭圆方程为![]() .
.
(2)当直线![]() 与
与![]() 轴垂直时,设直线
轴垂直时,设直线![]() 与椭圆相交于
与椭圆相交于![]() ,
, ![]() 两点.
两点.
则![]() ,
, ![]() ,由
,由![]() ,有
,有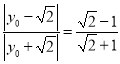 ,解得
,解得![]() 或
或![]() .
.
所以,若存在不同于点![]() 的定点
的定点![]() 满足条件,则
满足条件,则![]() 点的坐标只可能为
点的坐标只可能为![]() .
.
下面证明:对任意的直线![]() ,均有
,均有![]() .
.
当直线![]() 的斜率不存在时,由上可知,结论成立.
的斜率不存在时,由上可知,结论成立.
当直线![]() 的斜率存在时,可设直线
的斜率存在时,可设直线![]() 的方程为
的方程为![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() .
.
联立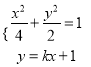 ,得
,得![]() .
.
其判别式![]() ,
,
∴![]() ,
, ![]()
∴![]() .
.
∴![]() ,
, ![]()
∴![]()
∴![]()

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目

