题目内容
已知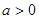 且
且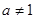 ,函数
,函数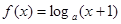 ,
,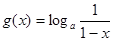 ,记
,记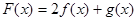
(1)求函数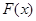 的定义域及其零点;
的定义域及其零点;
(2)若关于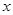 的方程
的方程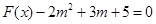 在区间
在区间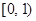 内仅有一解,求实数
内仅有一解,求实数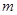 的取值范围.
的取值范围.
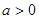 且
且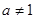 ,函数
,函数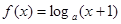 ,
,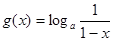 ,记
,记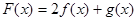
(1)求函数
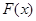 的定义域及其零点;
的定义域及其零点;(2)若关于
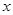 的方程
的方程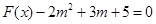 在区间
在区间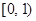 内仅有一解,求实数
内仅有一解,求实数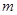 的取值范围.
的取值范围.(1) ,0;(2)
,0;(2)
 ,0;(2)
,0;(2)试题分析:(1)
 均有意义时,
均有意义时,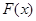 才有意义,即两个对数的真数均大于0.解关于x的不等式即可得出
才有意义,即两个对数的真数均大于0.解关于x的不等式即可得出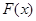 的定义域,函数
的定义域,函数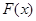 的零点,即
的零点,即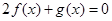 ,整理得
,整理得 ,对数相等时底数相同所以真数相等,得到
,对数相等时底数相同所以真数相等,得到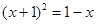 ,基础x即为函数
,基础x即为函数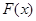 的零点(2)
的零点(2)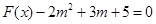 即
即 ,,应分
,,应分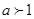 和
和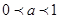 两种情况讨论
两种情况讨论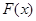 的单调性在求其值域。有分析可知
的单调性在求其值域。有分析可知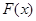 在这两种情况下均为单调函数,所以
在这两种情况下均为单调函数,所以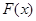 的值域即为
的值域即为 。解关于m的不等式即可求得m。所以本问的重点就是讨论
。解关于m的不等式即可求得m。所以本问的重点就是讨论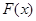 单调性求其值域。
单调性求其值域。试题解析:(1)解:(1)
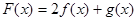
 (
(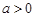 且
且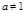 )
) ,解得
,解得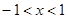 ,
, 所以函数
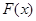 的定义域为
的定义域为 2分
2分令
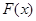
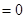 ,则
,则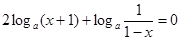 (*)方程变为
(*)方程变为 ,
,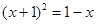 ,即
,即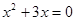
解得
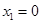 ,
, 3分
3分经检验
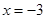 是(*)的增根,所以方程(*)的解为
是(*)的增根,所以方程(*)的解为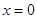 ,
,所以函数
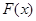 的零点为
的零点为 , 4分
, 4分(2)∵函数
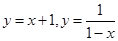 在定义域D上是增函数
在定义域D上是增函数∴①当
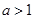 时,
时, 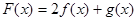 在定义域D上是增函数
在定义域D上是增函数②当
 时,函数
时,函数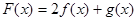 在定义域D上是减函数 6分
在定义域D上是减函数 6分问题等价于关于
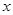 的方程
的方程 在区间
在区间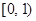 内仅有一解,
内仅有一解, ∴①当
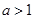 时,由(2)知,函数F(x)在
时,由(2)知,函数F(x)在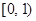 上是增函数
上是增函数∴
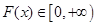 ∴只需
∴只需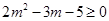 解得:
解得: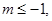 或
或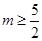
∴②当
 时,由(2)知,函数F(x)在
时,由(2)知,函数F(x)在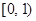 上是减函数
上是减函数∴
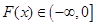 ∴只需
∴只需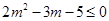 解得:
解得: 10分
10分综上所述,当
 时:
时: ;当
;当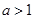 时,
时,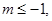 或
或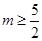 (12分)
(12分)
练习册系列答案
相关题目
 的解集是
的解集是 .
. (c为常数) .
(c为常数) .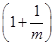 +loga
+loga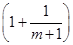 +…+loga
+…+loga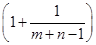 =logam+logan,求m、n的值.
=logam+logan,求m、n的值. )
)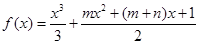 的两个极值点分别为
的两个极值点分别为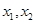 ,且
,且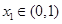 ,
,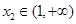 ,点
,点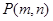 表示的平面区域为
表示的平面区域为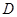 ,若函数
,若函数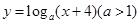 的图象上存在区域
的图象上存在区域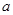 的取值范围为 .
的取值范围为 .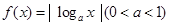 的定义域为
的定义域为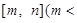
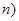 ,值域为
,值域为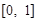 ,若
,若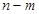 的最小值为
的最小值为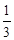 ,则实数
,则实数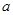 的值为 .
的值为 .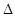 ABC中,若
ABC中,若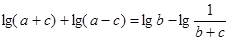 ,则A=( )
,则A=( )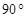
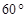
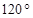
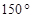
 ,则
,则 .
.