题目内容
已知等比数列{an}的公比q=3,前3项和S3=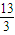 .
.(I)求数列{an}的通项公式;
(II)若函数f(x)=Asin(2x+φ)(A>0,0<φ<p<π)在
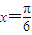 处取得最大值,且最大值为a3,求函数f(x)的解析式.
处取得最大值,且最大值为a3,求函数f(x)的解析式.
【答案】分析:(I)根据等比数列的前n项和的公式及q=3化简S3=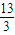 ,得到关于首项的方程,求出方程的解得到首项的值,然后根据首项和公比即可写出数列的通项公式;
,得到关于首项的方程,求出方程的解得到首项的值,然后根据首项和公比即可写出数列的通项公式;
(II)由(I)求出的通项公式求出a3的值,即可得到A的值,然后把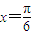 代入正弦函数中得到函数值等于1,根据φ的范围,利用特殊角的三角函数值即可求出φ的值,把φ的值代入即可确定出f(x)的解析式.
代入正弦函数中得到函数值等于1,根据φ的范围,利用特殊角的三角函数值即可求出φ的值,把φ的值代入即可确定出f(x)的解析式.
解答:解:(I)由q=3,S3=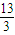 得:
得: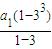 =
=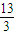 ,解得a1=
,解得a1= ,
,
所以an= ×3n-1=3n-2;
×3n-1=3n-2;
(II)由(I)可知an=3n-2,所以a3=3,
因为函数f(x)的最大值为3,所以A=3;
又因为当x=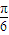 时,f(x)取得最大值,所以sin(2×
时,f(x)取得最大值,所以sin(2×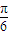 +φ)=1,
+φ)=1,
由0<φ<π,得到φ=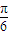 .
.
则函数f(x)的解析式为f(x)=3sin(2x+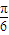 ).
).
点评:此题考查学生灵活运用等比数列的前n项和的公式及通项公式化简求值,掌握正弦函数的图象与性质以及会利用待定系数法求函数的解析式,是一道中档题.
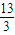 ,得到关于首项的方程,求出方程的解得到首项的值,然后根据首项和公比即可写出数列的通项公式;
,得到关于首项的方程,求出方程的解得到首项的值,然后根据首项和公比即可写出数列的通项公式;(II)由(I)求出的通项公式求出a3的值,即可得到A的值,然后把
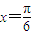 代入正弦函数中得到函数值等于1,根据φ的范围,利用特殊角的三角函数值即可求出φ的值,把φ的值代入即可确定出f(x)的解析式.
代入正弦函数中得到函数值等于1,根据φ的范围,利用特殊角的三角函数值即可求出φ的值,把φ的值代入即可确定出f(x)的解析式.解答:解:(I)由q=3,S3=
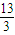 得:
得: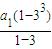 =
=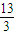 ,解得a1=
,解得a1= ,
,所以an=
 ×3n-1=3n-2;
×3n-1=3n-2;(II)由(I)可知an=3n-2,所以a3=3,
因为函数f(x)的最大值为3,所以A=3;
又因为当x=
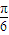 时,f(x)取得最大值,所以sin(2×
时,f(x)取得最大值,所以sin(2×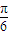 +φ)=1,
+φ)=1,由0<φ<π,得到φ=
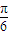 .
.则函数f(x)的解析式为f(x)=3sin(2x+
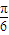 ).
).点评:此题考查学生灵活运用等比数列的前n项和的公式及通项公式化简求值,掌握正弦函数的图象与性质以及会利用待定系数法求函数的解析式,是一道中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目