题目内容
用总长为14.8米的钢条制成一个长方体容器的框架,如果所制的容器的底面的长比宽多0.5米,那么高为多少时容器的容器最大?并求出它的最大容积.
容器高为1.2m时容器的容积最大,最大容积为1.8m3.
解析试题分析:令容器底面宽为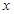 m,则长为(x+0.5)m,高为(3.2-2x)m,由实际意义可得0<x<1.6,由长方体体积写出容积
m,则长为(x+0.5)m,高为(3.2-2x)m,由实际意义可得0<x<1.6,由长方体体积写出容积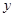 的表达式
的表达式 ,求导得
,求导得 ,进而求得0<x<1时,
,进而求得0<x<1时,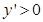 ;1<x<1.6时,
;1<x<1.6时,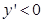 ,可知当
,可知当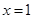 时
时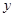 有最大值,求之得最大容积.
有最大值,求之得最大容积.
解:设容器底面宽为x m,则长为(x+0.5)m,高为(3.2-2x)m,
由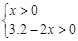 解得0<x<1.6, 3分
解得0<x<1.6, 3分
设容器的容积为y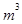 ,
,
则有y=x(x+0.5)(3.2-2x)= 6分
6分 ,
,
令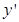 =0,即
=0,即 ,
,
解得x=1,或x= (舍去). 8分
(舍去). 8分
∵0<x<1时,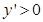 ;1<x<1.6时,
;1<x<1.6时,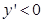 ,
,
∴在定义域(0,1.6)内x=1是唯一的极值点,且是极大值点,
∴当x=1时,y取得最大值为1.8, 10分
此时容器的高为3.2-2=1.2m,
因此,容器高为1.2m时容器的容积最大,最大容积为1.8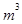 . 12分
. 12分
考点:利用导数求函数的最值,函数的应用.

练习册系列答案
相关题目
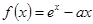 (
( 为常数)的图象与
为常数)的图象与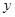 轴交于点
轴交于点 ,曲线
,曲线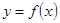 在点
在点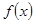 的极值;
的极值;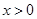 时,
时,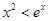 ;
; ,总存在
,总存在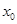 ,使得当
,使得当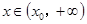 ,恒有
,恒有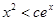 .
.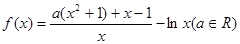 .
. 时,讨论
时,讨论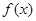 的单调性;
的单调性;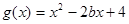 ,当
,当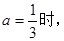 若对任意
若对任意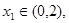 存在
存在 使
使 求实数
求实数 的取值范围。
的取值范围。 (
(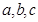 是常数)在
是常数)在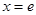 处的切线方程为
处的切线方程为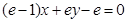 ,且
,且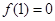 .
.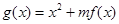 (
(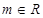 )在区间
)在区间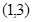 内不是单调函数,求实数
内不是单调函数,求实数 的取值范围.
的取值范围. (
( 的单位为:秒,
的单位为:秒, 的单位为:米/秒)的速度作变速直线运动,求该物体从时刻t=0秒至时刻 t=5秒间运动的路程?
的单位为:米/秒)的速度作变速直线运动,求该物体从时刻t=0秒至时刻 t=5秒间运动的路程? .
. 时,讨论函数
时,讨论函数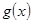 的单调性;
的单调性; 时,在函数
时,在函数 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为 ,试探究函数
,试探究函数 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系? 时
时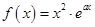 (
(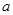 为小于
为小于 的常数).
的常数). 时,求函数
时,求函数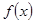 的单调区间;
的单调区间;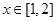 使不等式
使不等式 成立,求实数
成立,求实数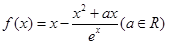 .
.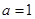 时,证明:当
时,证明:当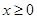 时,
时,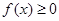 ;
;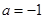 时,证明:
时,证明: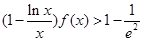 .
.