��Ŀ����
20����֪����C1��$\left\{\begin{array}{l}{x=8cost}\\{y=3sint}\end{array}\right.$��tΪ��������������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ������C2�ļ����귽�̦�=$\frac{7}{cos��-2sin��}$����PΪ����C1�ϵĵ㣬��Q�ļ�����Ϊ��4$\sqrt{2}$��$\frac{3��}{4}$������PQ�е�M������C2�ϵĵ�ľ������Сֵ��$\frac{8\sqrt{5}}{5}$������ ����$\left\{\begin{array}{l}{x=��cos��}\\{y=��sin��}\end{array}\right.$������C2�ļ����귽�̦�=$\frac{7}{cos��-2sin��}$����Ϊֱ�����귽�̣�����PΪ����C1�ϵĵ㣬����P��$\left\{\begin{array}{l}{x=8cost}\\{y=3sint}\end{array}\right.$��tΪ����������Q�ļ�����Ϊ��4$\sqrt{2}$��$\frac{3��}{4}$������Ϊֱ������Q��-4��4�����ɵ�PQ�е�M��4cost-2��$\frac{3sint+4}{2}$���������õ㵽ֱ�ߵľ��빫ʽ�����Ǻ����ĵ����Լ��ɵó���
��� �⣺����C1��$\left\{\begin{array}{l}{x=8cost}\\{y=3sint}\end{array}\right.$��tΪ����������Ϊ$\frac{{x}^{2}}{64}+\frac{{y}^{2}}{9}=1$��
����C2�ļ����귽�̦�=$\frac{7}{cos��-2sin��}$����Ϊx-2y-7=0��
��PΪ����C1�ϵĵ㣬����P��$\left\{\begin{array}{l}{x=8cost}\\{y=3sint}\end{array}\right.$��tΪ��������
��Q�ļ�����Ϊ��4$\sqrt{2}$��$\frac{3��}{4}$������Ϊֱ������Q��-4��4����
��PQ�е�M��4cost-2��$\frac{3sint+4}{2}$��������C2�ϵĵ�ľ���d=$\frac{|4cost-2-��3sint+4��-7|}{\sqrt{5}}$=$\frac{|5sin��t+����+13|}{\sqrt{5}}$$��\frac{13-5}{\sqrt{5}}$=$\frac{8\sqrt{5}}{5}$����sin��t+����=-1ʱȡ�Ⱥţ�
�ʴ�Ϊ��$\frac{8\sqrt{5}}{5}$��
���� ���⿼���˼����귽�̻�Ϊֱ�����귽�̡���Բ�IJ������̡��㵽ֱ�ߵľ��빫ʽ�����Ǻ����ĵ����ԣ�������������������������������е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | 2$\sqrt{5}$ | B�� | 2$\sqrt{6}$ | C�� | $\sqrt{34}$ | D�� | 2$\sqrt{7}$ |
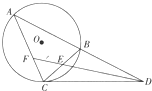 ��ͼ��ʾ����֪A��B��C���㶼�ڡ�O�ϣ�CD�ǡ�O�����ߣ�ֱ��AB��CD���ڵ�D��
��ͼ��ʾ����֪A��B��C���㶼�ڡ�O�ϣ�CD�ǡ�O�����ߣ�ֱ��AB��CD���ڵ�D��