题目内容
(本小题满分10分)在海岛 上有一座海拔1km的山峰,山顶设有一个观察站
上有一座海拔1km的山峰,山顶设有一个观察站 .有一艘轮船按一固定方向做匀速直线航行,上午11:00时,测得此船在岛北偏东
.有一艘轮船按一固定方向做匀速直线航行,上午11:00时,测得此船在岛北偏东 、俯角为
、俯角为 的
的 处,到11:10时,又测得该船在岛北偏西
处,到11:10时,又测得该船在岛北偏西 、俯角为
、俯角为 的
的 处.
处.

(1) 求船的航行速度;
(2) 求船从 到
到 行驶过程中与观察站
行驶过程中与观察站 的最短距离.
的最短距离.
 上有一座海拔1km的山峰,山顶设有一个观察站
上有一座海拔1km的山峰,山顶设有一个观察站 .有一艘轮船按一固定方向做匀速直线航行,上午11:00时,测得此船在岛北偏东
.有一艘轮船按一固定方向做匀速直线航行,上午11:00时,测得此船在岛北偏东 、俯角为
、俯角为 的
的 处,到11:10时,又测得该船在岛北偏西
处,到11:10时,又测得该船在岛北偏西 、俯角为
、俯角为 的
的 处.
处.
(1) 求船的航行速度;
(2) 求船从
 到
到 行驶过程中与观察站
行驶过程中与观察站 的最短距离.
的最短距离.(1)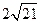 ;(2)
;(2)
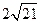 ;(2)
;(2)
解:⑴设船速为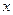 km/h,则
km/h,则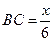 km.
km.
在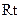 △
△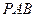 中,∠
中,∠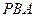 与俯角相等为30°,∴
与俯角相等为30°,∴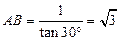 .
.
同理,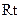 △
△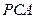 中,
中,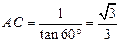 . (4分)
. (4分)
在△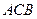 中,∠
中,∠ 15°+45°=60°,
15°+45°=60°,
∴由余弦定理得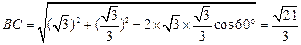 ,
,
∴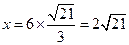 km/h,∴船的航行速度为
km/h,∴船的航行速度为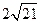 km/h. (6分)
km/h. (6分)
⑵(方法一)作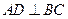 于点
于点 ,∴当船行驶到点
,∴当船行驶到点 时,
时,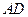 最小,从而
最小,从而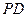 最小.
最小.
此时, . (10分)
. (10分)
∴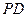 =
=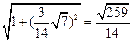 .
.
∴船在行驶过程中与观察站 的最短距离为
的最短距离为 km. (12分)
km. (12分)
(方法二)由⑴知在△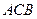 中,由正弦定理
中,由正弦定理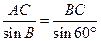 ,
,
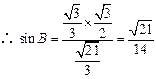 . (8分)
. (8分)
作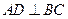 于点
于点 ,∴当船行驶到点
,∴当船行驶到点 时,
时,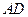 最小,从而
最小,从而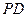 最小.
最小.
此时,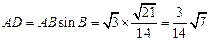 . (10分)
. (10分)
∴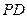 =
= .
.
∴船在行驶过程中与观察站 的最短距离为
的最短距离为 km. (12分)
km. (12分)
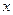 km/h,则
km/h,则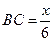 km.
km.在
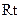 △
△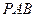 中,∠
中,∠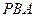 与俯角相等为30°,∴
与俯角相等为30°,∴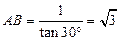 .
.同理,
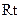 △
△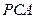 中,
中,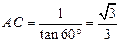 . (4分)
. (4分)在△
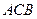 中,∠
中,∠ 15°+45°=60°,
15°+45°=60°,∴由余弦定理得
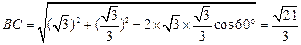 ,
,∴
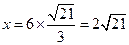 km/h,∴船的航行速度为
km/h,∴船的航行速度为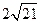 km/h. (6分)
km/h. (6分)⑵(方法一)作
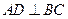 于点
于点 ,∴当船行驶到点
,∴当船行驶到点 时,
时,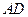 最小,从而
最小,从而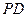 最小.
最小.此时,
 . (10分)
. (10分)∴
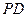 =
=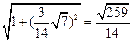 .
.∴船在行驶过程中与观察站
 的最短距离为
的最短距离为 km. (12分)
km. (12分)(方法二)由⑴知在△
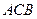 中,由正弦定理
中,由正弦定理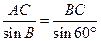 ,
,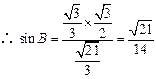 . (8分)
. (8分)作
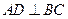 于点
于点 ,∴当船行驶到点
,∴当船行驶到点 时,
时,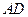 最小,从而
最小,从而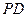 最小.
最小.此时,
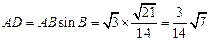 . (10分)
. (10分)∴
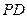 =
= .
.∴船在行驶过程中与观察站
 的最短距离为
的最短距离为 km. (12分)
km. (12分)
练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 中,
中, ,中线
,中线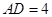 ,则
,则 边的取值范围是( ).
边的取值范围是( ).



 中,已知
中,已知 ,
, ,
, ,则
,则



 中,若
中,若 ,则
,则 等于
等于



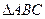 中,
中,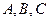 的对边分别是
的对边分别是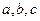 ,已知
,已知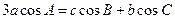 .
.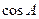 的值;
的值;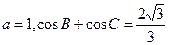 ,求边
,求边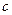 的值.
的值.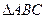 中,内角A,B,C的对边分别是
中,内角A,B,C的对边分别是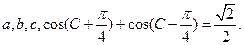
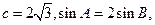 求a,b.
求a,b. 锐角
锐角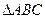 中,
中,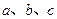 分别是角
分别是角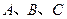 的
的 对边,
对边,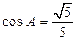 ,
,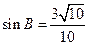 .
. 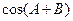 的值
的值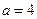 ,求
,求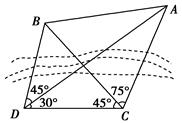
 中,∠A:∠B:∠C=1:2:3,则
中,∠A:∠B:∠C=1:2:3,则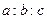 的值为
的值为 



