题目内容
(2013•江西)函数y=sin2x+2
sin2x最小正周期T为
| 3 |
π
π
.分析:函数解析式第二项利用二倍角的余弦函数公式化简,整理后利用两角和与差的正弦函数公式化为一个角的正弦函数,找出ω的值,代入周期公式即可求出函数的最小正周期.
解答:解:y=sin2x+2
×
=sin2x-
cos2x+
=2(
sin2x-
cos2x)+
=2sin(2x-
)+
,
∵ω=2,∴T=π.
故答案为:π
| 3 |
| 1-cos2x |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 3 |
| 3 |
∵ω=2,∴T=π.
故答案为:π
点评:此题考查了三角函数的周期性及其求法,涉及的知识有:二倍角的余弦函数公式,两角和与差的正弦函数公式,熟练掌握公式是解本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
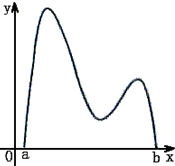 (2013•安徽)函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…xn,使得
(2013•安徽)函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…xn,使得