题目内容
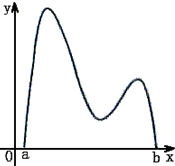（2013•安徽）函数y=f（x）的图象如图所示，在区间[a，b]上可找到n（n≥2）个不同的数x1，x2，…，xn，使得| f(x1) |
| x1 |
| f(x2) |
| x2 |
| f(xn) |
| xn |
分析：由
表示（x，f（x））点与原点连线的斜率，结合函数y=f（x）的图象，数形结合分析可得答案．
| f(x) |
| x |
解答：解：∵
表示（x，f（x））点与原点连线的斜率
若
=
=…=
，
则n可以是2，如图所示：
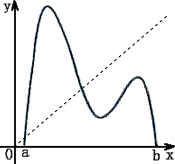
n可以是3，如图所示：
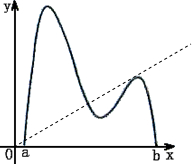
n可以是4，如图所示：
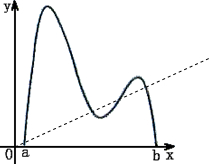
但n不可能大于4
故选B
| f(x) |
| x |
若
| f(x1) |
| x1 |
| f(x2) |
| x2 |
| f(xn) |
| xn |
则n可以是2，如图所示：
n可以是3，如图所示：
n可以是4，如图所示：
但n不可能大于4
故选B
点评：本题考查的知识点是斜率公式，正确理解
表示（x，f（x））点与原点连线的斜率是解答的关键．
| f(x) |
| x |
练习册系列答案
相关题目