题目内容
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前n项和为
的前n项和为![]() , ,且
, ,且![]() ,
,![]() ,.在①
,.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]()
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)分别选择条件①②③,结合等差、等比数列的通项公式,以及![]() 和
和![]() 的关系,即可求得数列
的关系,即可求得数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)由(1)求得![]() ,结合等差、等比数列的前
,结合等差、等比数列的前![]() 项和公式,利用错位相减,即可求解.
项和公式,利用错位相减,即可求解.
(1)若选①:![]() ,设等差数列
,设等差数列![]() 的公差为
的公差为![]() ,
,
由![]() ,
,![]() ,可得
,可得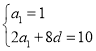 ,解得
,解得![]() ,
,
所以![]() ,
,
又由![]() ,
,
当![]() 时,由
时,由![]() ,则有
,则有![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,整理得
,整理得![]() ,即
,即![]() ,
,
所以![]() 是以2为首项,2为公比的等比数列,
是以2为首项,2为公比的等比数列,
所以![]() .
.
(2)由(1)知![]() ,则
,则![]() ,
,
所以![]()
![]() ,
,
所以![]() .
.
(1)若选②:![]() ,设等差数列
,设等差数列![]() 的公差为d,
的公差为d,
由![]() ,
,![]() ,可得
,可得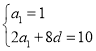 ,解得
,解得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
设等比数列![]() 的公比为
的公比为![]() ,
,
因为![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
所以![]() .
.
(2)由(1)知![]() ,则
,则![]() ,
,
所以![]()
![]() ,
,
所以![]() .
.
(1)若选③:![]() ,设等差数列
,设等差数列![]() 的公差为
的公差为![]() ,
,
由![]() ,
,![]() ,可得
,可得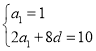 ,解得
,解得![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() ,
,
当![]() ,得
,得![]() ,即
,即![]() ,解得
,解得![]() ,所以
,所以![]() .
.
(2)由(1)知![]() ,则
,则![]() ,
,
所以![]()
![]() ,
,
所以![]() .
.

【题目】现从某学校中选出![]() 名学生,统计了
名学生,统计了![]() 名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.
名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.

(1)写出![]() 的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
(2)假设![]() ,则户外运动时长为
,则户外运动时长为![]() 的学生中,男生人数比女生人数多的概率.
的学生中,男生人数比女生人数多的概率.
(3)若![]() ,完成下列
,完成下列![]() 列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
每周户外运动时间不少于130分钟 | 每周户外运动时间少于130分钟 | 合计 | |
男 | |||
女 | |||
合计 |
附: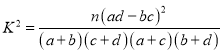 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某省从2021年开始,高考采用取消文理分科,实行“![]() ”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的
”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的![]() 列联表.
列联表.
性别 | 选择物理 | 选择历史 | 总计 |
男生 | ________ | 50 |
|
女生 | 30 | ________ |
|
总计 | ________ | ________ | 200 |
(1)求![]() ,
,![]() 的值;
的值;
(2)请你依据该列联表判断是否有99.5%的把握认为选择科目与性别有关?说明你的理由.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: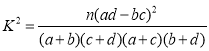 ,其中
,其中![]() .
.