题目内容
设{an}为等比数列,Sn为其前n项和,已知an+1=2Sn+1.
(Ⅰ)求{an}的通项公式;
(Ⅱ)求数列{nan}的前n项和Hn.
(Ⅰ)求{an}的通项公式;
(Ⅱ)求数列{nan}的前n项和Hn.
(Ⅰ)∵an+1=2Sn+1,
∴an=2Sn-1+1,(n≥2)
∴an+1-an=2(Sn-Sn-1)=2an,(n≥2)
∴an+1=3an,(n≥2),
∴q=3.
对于an+1=2Sn+1令n=1,可得a2=2a1+1=3a1,
解得a1=1,
∴an=3n-1.
(Ⅱ)nan=n•3n-1,
Hn=1+2•3+3•32+…+n•3n-1 ①
3Hn=3+2•32+3•33+…+n•3n ②
①-②得-2Hn=1+3+32+…+3n-1-n•3n=
-n•3n,
∴Hn=
×3n+
.
∴an=2Sn-1+1,(n≥2)
∴an+1-an=2(Sn-Sn-1)=2an,(n≥2)
∴an+1=3an,(n≥2),
∴q=3.
对于an+1=2Sn+1令n=1,可得a2=2a1+1=3a1,
解得a1=1,
∴an=3n-1.
(Ⅱ)nan=n•3n-1,
Hn=1+2•3+3•32+…+n•3n-1 ①
3Hn=3+2•32+3•33+…+n•3n ②
①-②得-2Hn=1+3+32+…+3n-1-n•3n=
| 1-3n |
| 1-3 |
∴Hn=
| 2n-1 |
| 4 |
| 1 |
| 4 |

练习册系列答案
相关题目
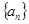 的前
的前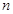 项和
项和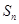 ,且
,且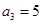 ,
,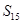 =225
=225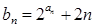 ,求数列
,求数列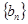 的前
的前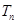 .
.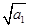 +
+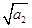 +…+
+…+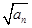 =n2+3n(n∈N*),则
=n2+3n(n∈N*),则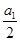 +
+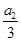 +…+
+…+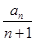 =________.
=________.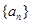 的通项公式
的通项公式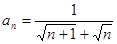 ,它的前n项和为
,它的前n项和为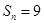 ,则
,则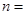 _________.
_________. 已知它的前n项和Sn=6,则项数n等于 .
已知它的前n项和Sn=6,则项数n等于 .