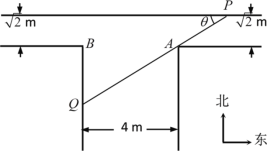
题目内容
【题目】对任意实数
给出下列命题:①“
”是“
”的充要条件;②“
是无理数”是“
是无理数”的充要条件;③“
”是“
”的充分条件;④“
”是“
”的必要条件.其中真命题的个数是( )
A.1B.2C.3D.4
【答案】B
【解析】
根据充要条件的定义对题目中的四个答案逐一进行分析即可得到答案．
∵①中“
”
“
”为真命题，
但当
时，“” “”为假命题，
故“”是“”的充分不必要条件，故①为假命题；
∵②中“
是无理数”“
是无理数”为真命题，
“是无理数”“是无理数”也为真命题，
故“是无理数”是“是无理数”的充要条件，故②为真命题；
∵③中“
”“
”为假命题，
“”“”也为假命题，
故“”是“”即不充分也不必要条件，故③为假命题；
∵④中
，故“
”是“
”的必要条件，
故④为真命题．故真命题的个数为2
故选：B
【题目】某校的一个社会实践调查小组，在对该校学生的良好“用眼习惯”的调查中，随机发放了120分问卷.对收回的100份有效问卷进行统计，得到如
下列联表：
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
（1）现按女生是否能做到科学用眼进行分层，从45份女生问卷中抽取了6份问卷，从这6份问卷中再随机抽取3份，并记其中能做到科学用眼的问卷的份数
，试求随机变量的分布列和数学期望；
（2）若在犯错误的概率不超过
的前提下认为良好“用眼习惯”与性别有关，那么根据临界值表，最精确的的值应为多少？请说明理由.
附：独立性检验统计量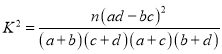
，其中
.
独立性检验临界值表：
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
【题目】某中学某社团为研究高三学生课下钻研数学时间与数学考试中的解答题得分的关系，随机调查了某中学高三某班
名学生每周课下钻研数学时间
(单位：小时)与高三下学期期中考试数学解答题得分
，数据如下表：
| 2 | 4 | 6 | 8 | 10 | 12 |
| 30 | 38 | 44 | 48 | 50 | 54 |
（1）根据上述数据，求出数学考试中的解答题得分与该学生课下钻研数学时间的线性回归方程，并预测某学生每周课下钻研数学时间为
小时其数学考试中的解答题得分；
（2）从这人中任选
人，求人中至少有
人课下钻研数学时间不低于
小时的概率.
参考公式：
，其中
，
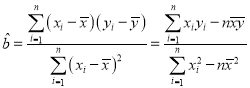；参考数据：
