题目内容
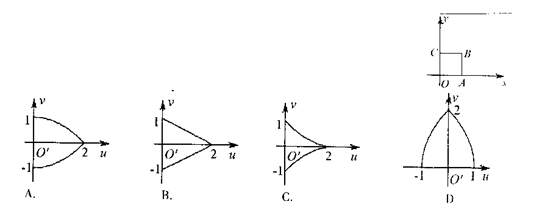
如右图,在平面直角坐标系xoy 中,A(1,0),B(1,1),
C(0,1),映射f 将xOy 平面上的点P(x,y)对应到另一 个平面直角坐标系uo′v 上的点P′(2xy,x2 – y2),则当点
P 沿着折线A—B—C 运动时,在映射f 的作用下,动点P′的
轨迹是( )
|
P 沿着折线A—B—C 运动时,在映射f 的作用下,动点P′的
轨迹是( )
A
分析:本题考查的知识点是映射的定义,函数的图象及轨迹方程,根据映射f将xOy平面上的点P(x,y)对应到另一个平面直角坐标系uO’v上的点P’(2xy,x2-y2),我们分点P沿着线段AB和线段BC运动两种情况分析讨论,即可得到动点P’的轨迹.
解:点P沿着线段AB运动时
X=1,Y∈[0,1]
此时P’(2xy,x2-y2)的坐标为(2y,1-y2),消掉参数y后,得到动点P’的轨迹是y=-
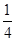 x2+1(x∈[0,2])
x2+1(x∈[0,2])点P沿着线段BC运动时
X∈[0,1],Y=1
此时P’(2xy,x2-y2)的坐标为(2x,x2-1),消掉参数x后,得到动点P’的轨迹是
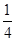 x2-1(x∈[0,2])
x2-1(x∈[0,2])故动点P’的轨迹是
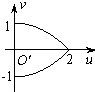
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
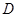 的函数
的函数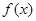 ,如果对任意的
,如果对任意的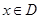 ,存在正数
,存在正数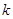 ,有
,有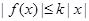 成立,
成立,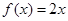 ;(2)
;(2)
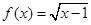 ;(4)
;(4) ;其中是“倍约束函数”的是 ( )
;其中是“倍约束函数”的是 ( )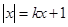 有负根而无正根,则实数k的取值范围是 ( )
有负根而无正根,则实数k的取值范围是 ( )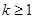
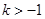
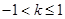
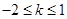
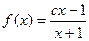 (
(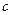 为常数).
为常数).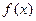 的零点, 求
的零点, 求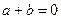 , 求
, 求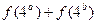 的值;
的值;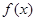 的图像如图所示,则
的图像如图所示,则
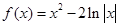
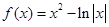
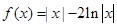
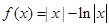
 5件.
5件. 当该商场销售此服装的日销售量达到150件以上时,社会上就流行,问该款服装在社会上流行是否超过14天?并说明理由.
当该商场销售此服装的日销售量达到150件以上时,社会上就流行,问该款服装在社会上流行是否超过14天?并说明理由.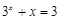 的解所在的区间为
的解所在的区间为 唯一的一个零点同时在区间
唯一的一个零点同时在区间 内,那么下列命题中正确的是( ).
内,那么下列命题中正确的是( ).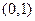 内没有零点
内没有零点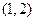 内有零点
内有零点
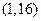 内有零点
内有零点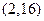 内没有零点
内没有零点